Modeling with missing data/latent variables
Stat 221, Lecture 9
Missing data and latent variables
Similar, but different.
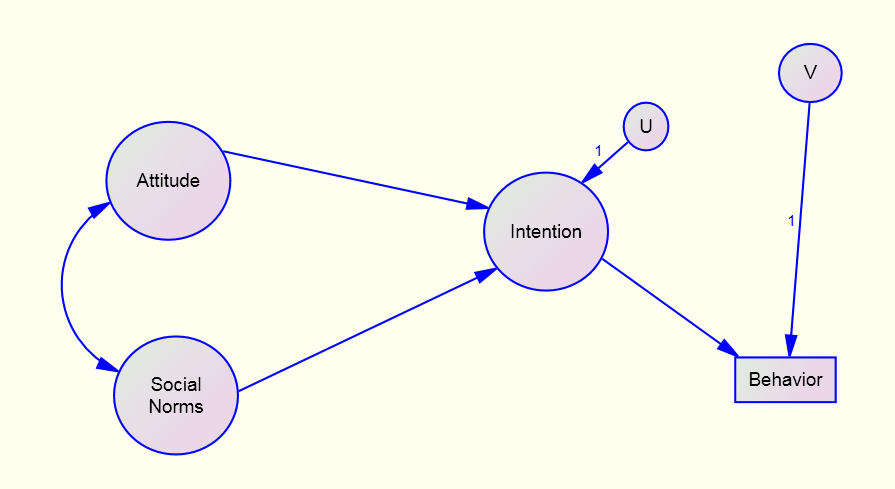
Where we are
Latent variables
- A tool for modeling.
- Example: ignorant and health aware intentions and running.
$$Z \sim \rr{Beta}(\alpha,\beta), \rr{ } Y_i \given Z \sim \rr{Bernoulli}(L_i)$$
Graphical representation
- Need to have many observations to infer a parameter.
- Let's look at this model's graphical representation.
The running man model
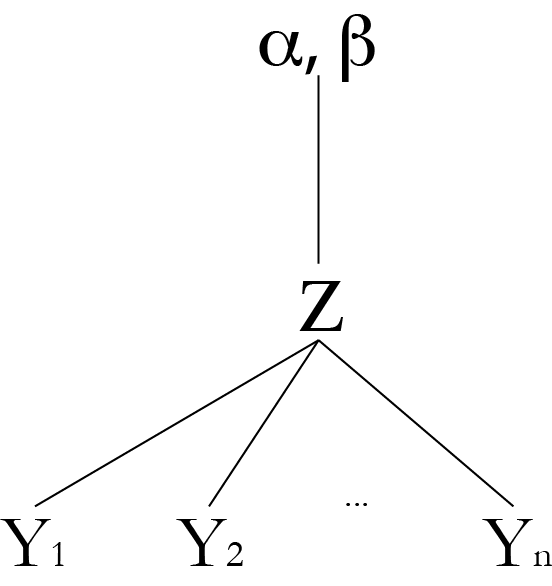
Example: likelihood
$$\begin{align}L(\{ \alpha, & \beta\}\given Y, Z) \\ &\propto \prod_{i=1}^n\frac{1}{\rr{B}(\alpha,\beta)}\, z^{y_i + \alpha-1}(1-z)^{1 - y_i + \beta-1}\end{align}$$
Problems with this model?
Example: Bayesian interpretation
$$\begin{align}p(\{ \alpha, & \beta, Z\}\given Y) \\ &\propto \prod_{i=1}^n\frac{1}{\rr{B}(\alpha,\beta)}\, z^{y_i + \alpha-1}(1-z)^{1 - y_i + \beta-1}\end{align}$$
Still suffers from the same problems. Solution: set \\( \alpha, \beta \\) to some values (hyperparameters).
Final Bayesian interpretation
Set \\( \alpha =1, \beta = 1 \\).
$$\begin{align}p(Z\given Y) \propto \prod_{i=1}^n z^{y_i}(1-z)^{1 - y_i}\end{align}$$
This looks like the likelihood function if \\( Z \\) is a parameter instead of a random variable.
Look at more people
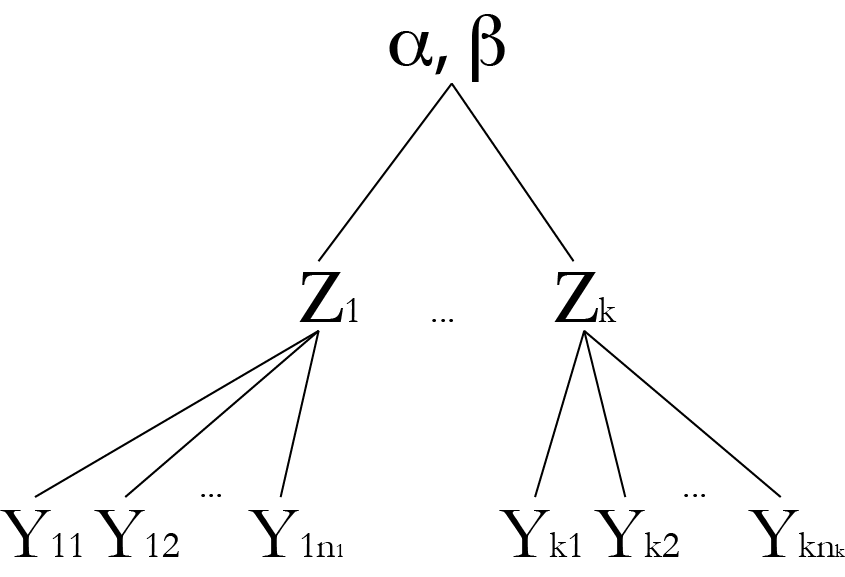
Now we may care about the prior on \\( Z \\)
- Because now we have replication of sporty/lazy variables.
- Can now formulate the model both with latent variables and just with parameters.
The new likelihood
$$\begin{align}L(& \{ \alpha, \beta\}\given Y, Z) \\ &\propto \prod_{i=1}^k\prod_{j=1}^{n_i}\frac{1}{\rr{B}(\alpha,\beta)}\, z_i^{y_{ij} + \alpha-1}(1-z_i)^{1 - y_{ij} + \beta-1}\end{align}$$
Look at effects of media
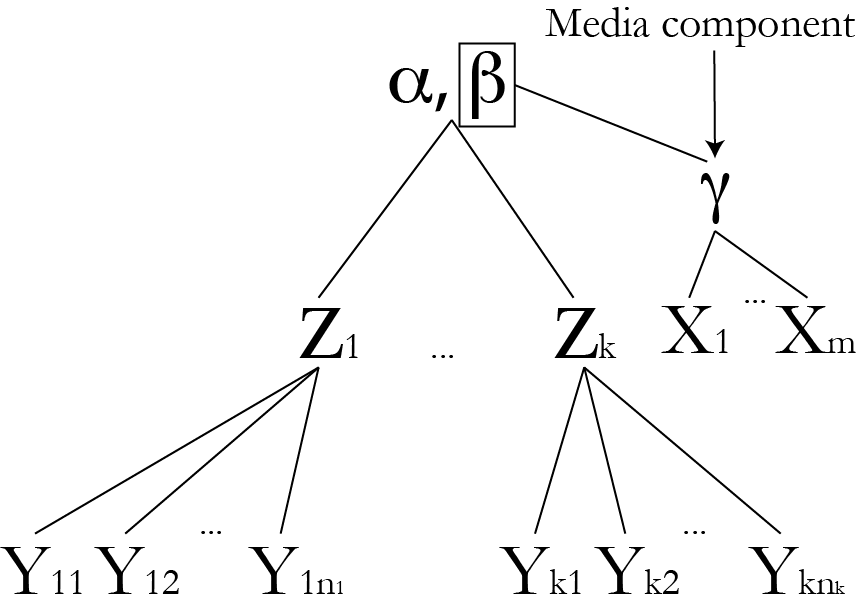
Does the structure allow to infer parameters from data?
- Are there many data points to infer each unknown?
- Does the whole model make sense?
Bayesian or frequentist approach
- Likelihood surface carries the main signal.
- Can choose point estimation/full simulation.
- Point estimation can deal with missing data.
Missing data
- Assume probabilistic mechanism of missingness.
- We observe part of the data, part is not there.
- We do not observe a whole variable.
- Ignorable and non-ignorable missing data.
- Example: what if on some days, we don't get to observe whether the subject ran or not?
Data and missingness indicator
- Actual data is \\( (Y, M) \\).
- We then need to consider the full likelihood for inference: $$L(\theta, \psi \given Y, M)$$
- See Little and Rubin pp. 117-124.
Example: censored exponential
- Observe lifespan of lightbulbs \\( Y_i \sim \rr{Expo}(\theta) \\).
- Lightbulbs get replaced at time \\( c \\).
- We'd like to make inferences about \\( \theta \\).
Example: likelihood
$$\begin{align}L(\theta & \given Y_{\rr{obs}}, M ) \propto f ( Y_{\rr{obs}}, M \given \theta) \\ & = \prod_{i=1}^r f(y_i, M_i \given \theta) \cdot \prod_{i=r+1}^n f(M_i \given \theta) \\ & = \theta^{-r} exp \left( -\sum_{i=1}^r\frac{y_i}{\theta}\right)exp \left( -\frac{(n-r)c}{\theta}\right)\end{align}$$
Different likelihoods
Complete-data, or full likelihood $$L(\theta \given Y_{\rr{obs}}, Y_{\rr{mis}}) \propto f_\theta\left(y_{\rr{obs}},y_{\rr{mis}}\right)$$
Observed-data likelihood $$L(\theta \given Y_{\rr{obs}}) \propto \int f_\theta\left(y_{\rr{obs}},y_{\rr{mis}}\right)dy_{\rr{mis}}$$
Ignorable missing data mechanism: can use observed-data likelihood.
Issue
- Often \\( f_\theta\left(y_{\rr{obs}},y_{\rr{mis}}\right)\\) doesn't integrate nicely.
- This is resolved by multiple imputation, EM, and MCMC variants.
- More on MCMC and EM soon.
Modeling with missing data/latent variables
Fraction of missing data
Large
Small
Latent variables
Posit a model
Never happens
Missing data
Model-sensitive, area of current research
Sensitive but manageable
Other models: HMM
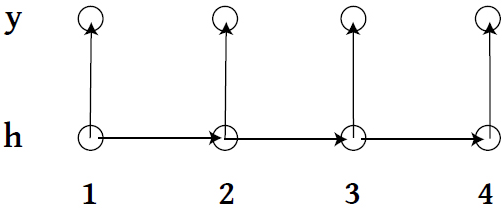
- \\(\{h_1, h_2, \ldots \} \\) live on discrete space, follow a Markov Process with a transition matrix \\( T_\theta \\).
- At time \\( t\\), state \\( h_t \\) emits observation \\( y_t \\) according to some specified model.
Running man HMM version
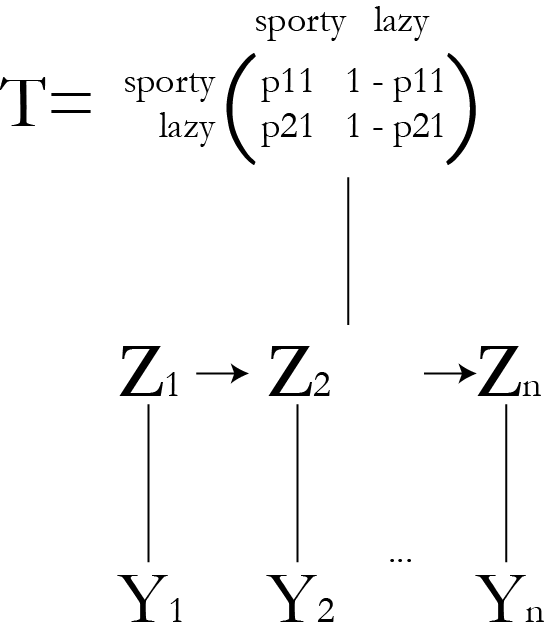
Likelihoods for HMM
- Observed-data $$L(\theta \given Y ) \propto \sum_{H} P_{\theta}(Y \given H)P_\theta(H)$$
- Complete-data $$\begin{align}L(\theta \given Y, H ) \propto & f_{\theta}(y_1 \given h_1)g_\theta(h_1) \cdot \\ & \prod_{i=2}^n f_{\theta}(y_i \given h_i)g_\theta(h_i \given h_{i-1})\end{align}$$
HMM running man complete-data likelihood
$$\begin{align} L(\theta \given Y, Z ) \propto & \left(\rr{Bern}(y_1|p_l)\right)^{z_1}\left(\rr{Bern}(y_1|p_s)\right)^{1-z_1} \\ \prod_{i=2}^n & \left(\rr{Bern}(y_i|p_l)\right)^{z_i}\left(\rr{Bern}(y_i|p_s)\right)^{1-z_i} \\ & \cdot T(z_i \given z_{i-1})\end{align}$$
AP model with missing data
$$\begin{align} X_i & = \begin{cases}Z_i &\rr{if observation }i\rr{ is missing,} \\ Y_i &\rr{if observation }i\rr{ is present}\end{cases} \\ X_{i} | X_{r(i)} & \sim \rr{N}\left(\rho_i X_{r(i)} + (1 - \rho_i) \mu, (1 - \rho_i^2) \sigma^2 \right)\\ X_i & \sim \rr{N} (\mu, \sigma^2) \rr{ if } i \rr{ is a seed} \end{align}$$
Likelihood
$$\begin{align}L(&\{ \mu, \rho, \sigma^2\} \given Y, Z) \propto \prod_{\{\rr{seeds } j\}} \frac{1}{\sqrt{\sigma^2}}e^{\frac{(x_j - \mu)^2}{2\sigma^2}} \cdot \\ & \prod_{\{\rr{referred }i\}} \frac{1}{\sqrt{(1-\rho^2)\sigma^2}}e^{\frac{(x_i - (\rho x_{r(i)} + (1 - \rho) \mu))^2}{2\sigma^2}}\end{align}$$
Is this complete or observed-data likelihood?
Assumptions?
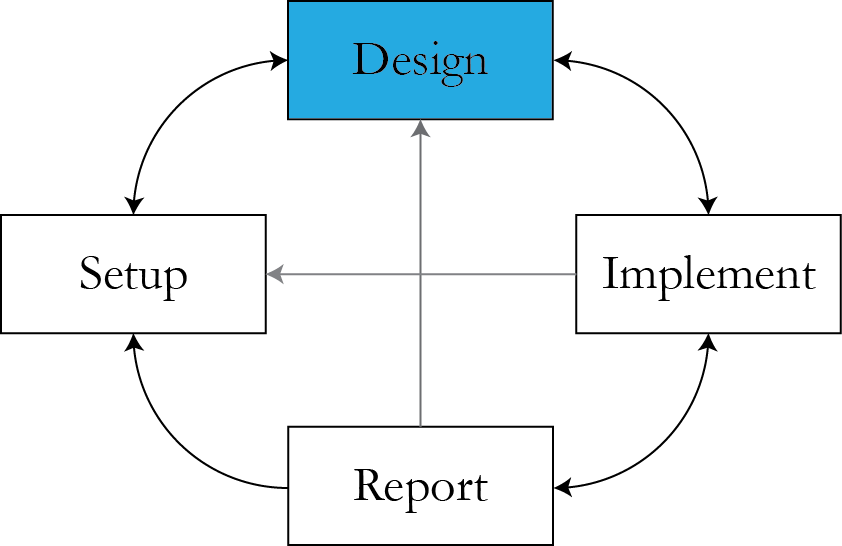
Designing models
Issues to consider
- The goal of the exercise.
- Interpretation-identifiability tradeoff.
- Implementation.
- Reporting.
Case study: marketing
- Users choose winning concepts in a series of windows where several concepts are presented at the same time.
- Client believes that users make choices based on defined elements of the concepts such as label font size, packaging shape, color etc.
- Moreover, for some users one set of features could be important, and for other users another set. We are willing to assume that there is some number of groups of users with common preferences.
Data
- User IDs, who rated what window.
- Every concept's features, quantitatively coded.
- IDs of winning objects for each window.
Model
- What is the dependence structure?
- Draw the graphical representation.
- Can the data inform the inference algorithm?
Model via representation
Rater \\( i\\), window \\( j \\), winning object \\( k \\).
Number of preference classes \\( N \\), number of objects/window \\( L \\).
$$Z_i \given \vec{p_i} \sim \rr{Multinom}_N(1, \vec{p_i})$$
$$C_{ij} \given Z_i, X \sim \rr{Multinom}_L(1, \vec{w}_{ij})$$
with
$$w_{ijl} \propto \rr{exp} \left\{ X_{jl} \beta_i\right\}$$
Complete-data likelihood
$$\begin{align} L& \left(\left\{ \vec{\beta}_n\right\} \given \left\{Z_{in}, C_{ijk}\right\} \right) \\ & \propto \prod_{i=1}^I \prod_{j \in J_i} \prod_{k \in K_{ij}} \prod_{n=1}^N \left( \frac{exp\left\{\vec{x}_{jk}' \vec{\beta}_n \right\}} {\sum_{l = 1}^{L_j} exp \left\{ \vec{x}_{jl}' \vec{\beta}_n \right\}} \right)^{Z_{in}} \end{align}$$
How can we improve the model?
- Collect more data?
- Smarter ways to use current data?
Announcements
- Problem set is 3 out.
Resources
- Slides nesterko.com/lectures/stat221-2012/lecture9
- Class website theory.info/harvardstat221
- Class Piazza piazza.com/class#spring2013/stat221
- Class Twitter twitter.com/harvardstat221
Final slide
- Next lecture: algorithms for missing data - EM.
