Stochastic optimization for inference, Odyssey
Stat 221, Lecture 8
Inference + data analysis
Where do inference & likelihood principle fit?
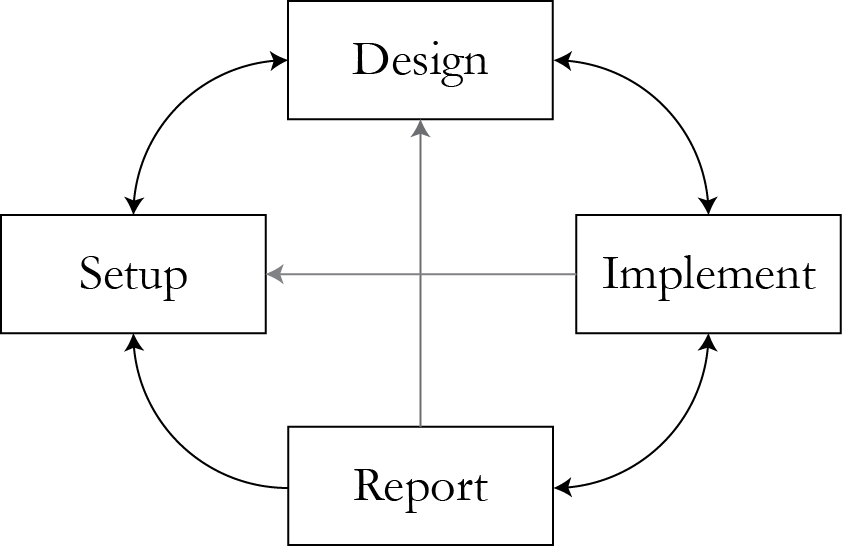
Think about tradeoffs
- Design-Implementation. Inference algorithm computing complexity.
- Design-Reporting. Validity of inference with the selected approach.
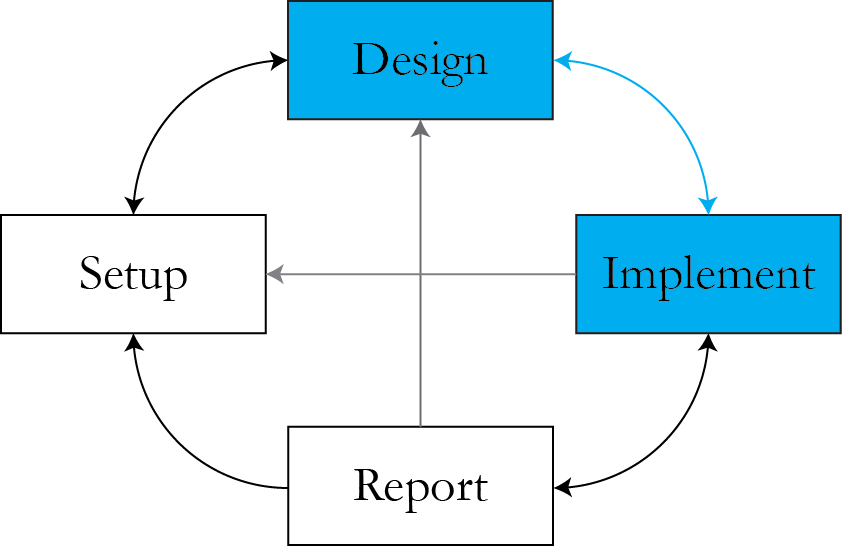
How is Observed Fisher Information misleading?
- Also, criticize the visualization!
- Student discussion - 5 min.
Likelihood and Information
Currently we are here
How to use the full likelihood surface?
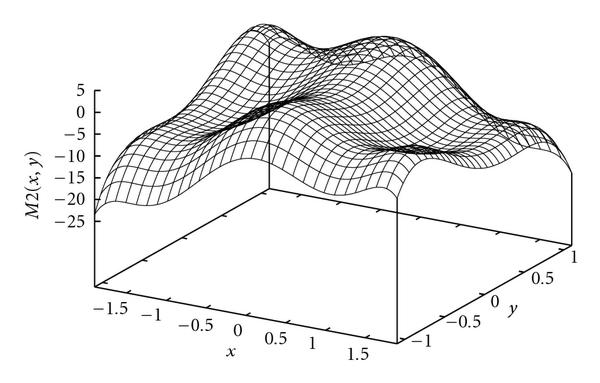
One approach
- Pretend that the likelihood surface is a pdf of the parameters and sample from it.
- This would provide usable information on the parameters of interest.
SNOTE: univariate Normal
Gaussian data \\( X \given \mu \sim \rr{Normal}(\mu, \sigma^2) \\), \\( \sigma^2 \\) known number.
$$L(\mu \given X) \propto \frac{1}{\sqrt{2\pi\sigma^2}} e^{ -\frac{(x-\mu)^2}{2\sigma^2} }$$
MLE \\( \hat{\mu}_{\rr{mle}} = x \\), Fisher Information \\( I(\mu) = 1 / \sigma^2\\).
Seems reasonable to pretend that $$\mu \given X \sim \rr{Normal}(x, \sigma^2)$$
Simulate and get information on \\( \mu \\).
Estimating parameters differently
- Switching to a Bayesian paradigm.
- Pretend that the likelihood function is pdf/pmf of parameters.
- This is often better, but sometimes leads to degeneracy.
Example: Binomial likelihood
$$L(p \given m) \propto p^m (1-p)^{n-m}$$
- If viewed as a pdf for \\( p \\), this is \\( \rr{Beta}( m + 1, n - m + 1) \\).
- We know its mean, variance, direct simulation is available.
- Simulate 1000 draws and run quantile on that.
Tradeoff: the good
Good for non-Gaussian likelihoods - better interval estimation.

Tradeoff: the bad
- Sometimes leads to improper distributions of parameters.
- Direct simulation is usually not available.
- Which one is worse?
Practical high-dimensional cases
- What if we have more than one parameter, and it is unclear how to simulate all of them from the joint density at the same time?
Correlated Bivariate Normal
$$\left.\left( \begin{array} dX \\ Y\end{array}\right)\right| \rr{ }\mu_x, \mu_y, \rho \sim \rr{N} \left( \left( \begin{array} d\mu_x \\ \mu_y\end{array}\right), \left( \begin{array} n1 & \rho \\ \rho & 1 \end{array} \right) \right)$$
Likelihood
$$\begin{align}L(\mu_x,& \mu_y, \rho \given x,y) = \frac{1}{2 \pi \sqrt{1-\rho^2}} \cdot \\ & e^{ -\frac{1}{2(1-\rho^2)}\left[ (x-\mu_x)^2 + (y-\mu_y)^2 - (x-\mu_x)(y-\mu_y) \right]}\end{align}$$
Can we simulate \\( \mu_x, \mu_y, \rho \\) jointly from here?
Gibbs philosophy
Divide and conquer.
In order to simulate parameter vector \\( \theta \\) from its pdf \\( g\\):
- Pick index \\( 1 \leq j \leq d \\).
- Pick a new value \\( \left.\theta_j\right.\\) according to \\( g(\theta_1, \ldots , \theta_{j-1} , \, \cdot \, , \theta_{j+1} , \ldots , \theta_d ) \\).
- Repeat.
Step 2 may be done using a Metropolis proposal rather than exactly (i.e. Metropolis-within-Gibbs).
Example: Normal likelihood
$$\begin{align}l(\{\sigma^2, \mu \} \given y) = & -\frac{1}{2}\ln(2\pi) - \frac{1}{2}\ln\sigma^2 \\ & - \frac{(y-\mu)^2}{2\sigma^2}\end{align}$$
- Distribution for \\( \mu \\) given \\( \sigma^2 \\): $$\mu \given \sigma^2 \sim \rr{Normal} \left( y, \sigma^2\right)$$
- What is the distribution of \\( \sigma^2 \\) given \\( \mu \\)?
Closer look
Inverse-Gamma distribution:
$$f(x; \alpha, \beta) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{-\alpha - 1}\exp\left(-\frac{\beta}{x}\right)$$
with \\( \alpha > 0 \\), \\( \beta > 0 \\)
Taking a log:
$$\rr{log}f(x; \alpha, \beta) = \rr{const} - (\alpha + 1) \rr{log}(x) -\frac{\beta}{x} $$
A problem
- \\( \sigma^2 \\) is almost Inverse-Gamma, but with \\( \alpha = - 1/2 \\).
- \\( L(\{\sigma^2, \mu \} \given y) \\) does not have a finite integral over \\( (0, \infty) \\).
- \\(l \\) is improper if viewed as a pdf for \\( \sigma^2 \\).
Fixing the problem
Sample from $$p(\{\sigma^2, \mu \} \given y) = \rr{c} - \frac{3}{2}\ln\sigma^2 - \frac{(y-\mu)^2}{2\sigma^2}$$
Old log-likelihood: $$l(\{\sigma^2, \mu \} \given y) = \rr{c} - \frac{1}{2}\ln\sigma^2 - \frac{(y-\mu)^2}{2\sigma^2}$$
We have just defined a prior
Posterior
$$p(\{\sigma^2, \mu \} | y) = \rr{const} + \rr{log}p(\sigma^2) + l(\{\sigma^2, \mu \} | y)$$
with
$$p(\sigma^2) \propto 1 / \sigma^2$$
The prior is an improper distribution!
Roles of prior
- Bringing in more information into the model (expert opinions/knowledge).
- Less well-known role: regularization.
- Regularization is good for numeric stability, "patching" the model.
Example: bivariate Normal
Posterior distribution: $$\left.\left( \begin{array} d\theta_1 \\ \theta_2\end{array}\right)\right| \rr{ }y \sim \rr{N} \left( \left( \begin{array} dy_1 \\ y_2\end{array}\right), \left( \begin{array} n1 & \rho \\ \rho & 1 \end{array} \right) \right)$$
Gibbs updates: $$\begin{align} \theta_1 \given \theta_2, y & \sim \rr{N} (y_1 + \rho (\theta_2 - y_2), 1 - \rho^2) \\ \theta_2 \given \theta_1, y & \sim \rr{N} (y_2 + \rho (\theta_1 - y_1), 1 - \rho^2)\end{align}$$
The AP model
$$$$\begin{align} Y_i \given Y_{r(i)} & \sim N \left(\rho Y_{r(i)} + (1 - \rho) \mu, (1 - \rho^2) \sigma^2 \right), \\Y_i & \sim N\left( \mu, \sigma^2 \right) \rr{ if } r(i)\rr{ doesn't exist}\end{align}$$$$
$$\begin{align}L(&\{ \mu, \rho, \sigma^2\} \given Y) \propto \prod_{\{\rr{seeds } j\}} \frac{1}{\sqrt{\sigma^2}}e^{\frac{(y_j - \mu)^2}{2\sigma^2}} \cdot \\ & \prod_{\{\rr{referred }i\}} \frac{1}{\sqrt{(1-\rho^2)\sigma^2}}e^{\frac{(y_i - (\rho y_{r(i)} + (1 - \rho) \mu))^2}{2\sigma^2}}\end{align}$$
Simulating parameters
- To initialize, choose initial values for \\(\{ \mu, \rho, \sigma^2\} \\).
- Draw members of \\(\{ \mu, \rho, \sigma^2\} \\) using Gibbs:
- Draw \\(\mu^{(n+1)}\\) and \\(\sigma^{2^{(n+1)}}\\) from their exact posterior distributions given observed data and current draws of other parameters.
- Draw \\( \rho^{(n+1)} \\) with a Metropolis jump on transformed space.
Distribution of \\(\sigma^2\\)
\\( \sigma^{2^{(n+1)}} \\) is Inverse-Gamma\\( (a, b) \\) with $$\begin{align} a = & \frac{n}{2} - 1, \\ b = &\frac{1}{2} \sum_{i \in I} \frac{1}{1 - \rho_i^{(n+1)^2}} \left(y_i^{(n+1)} - \left(\rho_i^{(n+1)} y_{r(i)}^{(n+1)} \right.\right. \\ & \left.\left.+ \left(1 - \rho_i^{(n+1)}\right)\mu^{(n+1)}\right)\right)^2\end{align}$$
More complicated: HMM
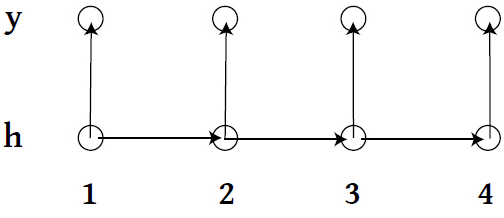
- \\(\{h_1, h_2, \ldots \} \\) live on discrete space, follow a Markov Process with a transition matrix \\( T_\theta \\).
- At time \\( t\\), state \\( h_t \\) emits observation \\( y_t \\) according to some specified model.
Gibbs for HMM?
- Observed-data $$L(\theta \given Y ) = \sum_{H} P_{\theta}(Y \given H)P_\theta(H)$$
- Complete-data $$\begin{align}L(\theta \given Y, H ) = & f_{\theta}(y_1 \given h_1)g_\theta(h_1) \cdot \\ & \prod_{i=2}^n f_{\theta}(y_i \given h_i)g_\theta(h_i \given h_{i-1})\end{align}$$
What could be the computational complexity?
Vicious circle
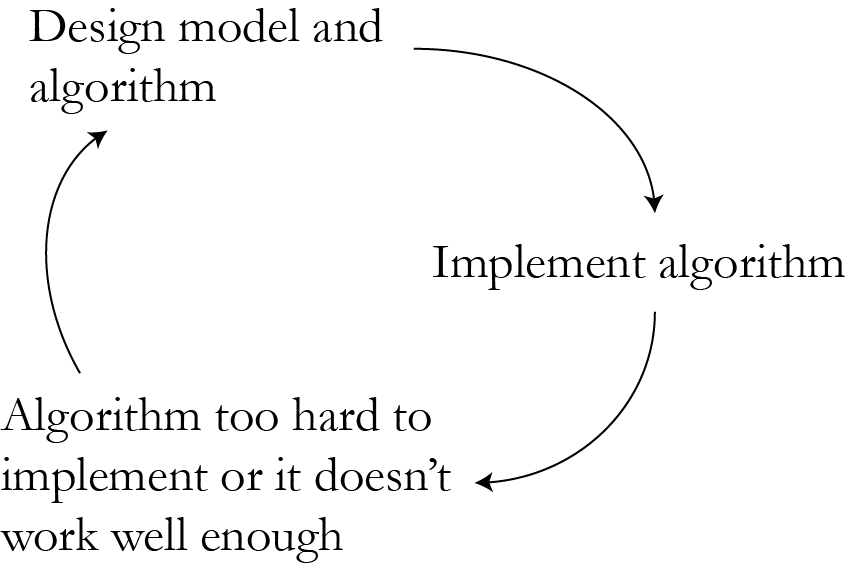
Cloud computing helps?

What it helps with
- Faster turnaround.
- Get more work done (sensitivity analysis, longer runs).
Price to pay
Announcements
Resources
- Slides nesterko.com/lectures/stat221-2012/lecture8
- Class website theory.info/harvardstat221
- Class Piazza piazza.com/class#spring2013/stat221
- Class Twitter twitter.com/harvardstat221
Final slide
- Next lecture: modeling and latent variables/missing data

