Likelihood principle, MLE foundations, Odyssey

Stat 221, Lecture 7

@snesterko

What data analysts do

Describe real world systems with models.

A Bernoulli model

$$Y_i \mathop{\sim}^{\rr{iid*}} \rr{Bernoulli}(p)$$

• What if the coin is unfair?

*Independent repetition is great.

Inferring parameters

• First state a statistical model.
• Assume the model describes something real: a system, a process, a population etc.
• Assume the inferred parameters describe real characteristics of the described entity.
• Hope that describing a system well leads to practical results.

Finally

• Use the Likelihood principle:

Given a statistical model, all information about the parameters is contained in the likelihood function.

Estimation with Maximum Likelihood

$$\hat{\theta}_{\rr{mle}} \mathop{\rightarrow}^p \theta_0, \rr{ } \rr{Var}\left(\hat{\theta}_{\rr{mle}}\right) \approx I^{-1} / n$$

Conditions:

• Identifiability.
• Number of nuisance parameters is limited.
• Increasing information.
• Others.

The result is asymptotic.

Definitions

MLE \\( \hat{\theta}_{\rr{mle}} \\): $$ \hat{\theta}_{\rr{mle}} = \rr{argmax}_\theta \left[ \log L\left(\theta \given y \right) \right]$$

Expected Fisher Information $$I(\theta)=\operatorname{E}_y \left[\left. \left(\frac{\partial}{\partial\theta} \log L(\theta \given y)\right)^2\right|\theta \right]$$

Reference

• A.C. Davison "Statistical Models" pp. 109-125.

Under differentiability

Expected Fisher Information \\( I(\theta) \\): $$I(\theta)=-\operatorname{E}_y \left[\left. \frac{\partial^2}{\partial\theta^2} \log L(\theta \given y)\right|\theta \right]$$

Let's show this.

Observed Fisher Information

$$ \mathcal{I}(\theta)=-\frac{\partial^2}{\partial\theta^2} \log L(\theta \given y) $$

It is the negative Hessian of the log-likelihood function.

Example: Exponential data

\\( Y_i \sim \rr{Expo} ( \lambda )\\) represent time to failure of lightbulbs.

Likelihood $$L \left( \lambda \given y \right) = \prod_{i=1}^n \lambda e^{-\lambda y_i}$$

Score \\( s ( \lambda \given y) = \sum_{i=1}^n \left({ 1 \over \lambda} - y_i \right)\\).

Observed Fisher Information (= Expected!) $$\mathcal{I}(\lambda) = { n \over \lambda^2 }$$

Example: Binomial data

\\( k \\) succcesses out of n trials: $$L(p \given y)=\frac{n!}{k!(n - k)!}p^k(1-p)^{n-k}$$

Score \\( s(p \given y)={\partial \over \partial p} \log L( p \given y) = \frac{k}{p}-\frac{n-k}{1-p}\\).

Expected Fisher Information $$\rr{Var}\left(s\right) =\operatorname{Var}(k)\left(\frac{1}{p}+\frac{1}{1-p}\right)^2 =\frac{n}{p(1-p)}$$

Let's obtain it via observed Fisher Information.

Analytic maximization to get MLE

• Binomial $$s(p \given y) = 0 \implies \hat{p}_{\rr{mle}} = {k \over n}$$
• Exponential $$s(\lambda \given y) = 0 \implies \hat{\lambda}_{\rr{mle}} = {1 \over \bar{y}}$$

Back to assumptions

Optimality conditions for the MLE:

• Identifiability.
• Number of nuisance parameters is limited.
• Increasing information.
• Others.

In practice

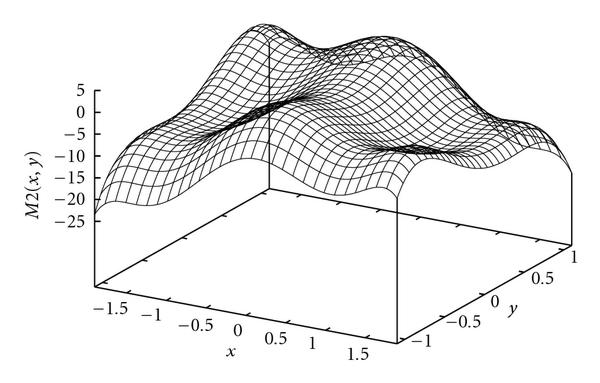
Examples

• HMMs.
• Missing data problems.
• Data not fitting the model well.
• Overparametrization.
• Pset 3.
• To a large extent, any modern applied data analysis problem.

For now, assume best case

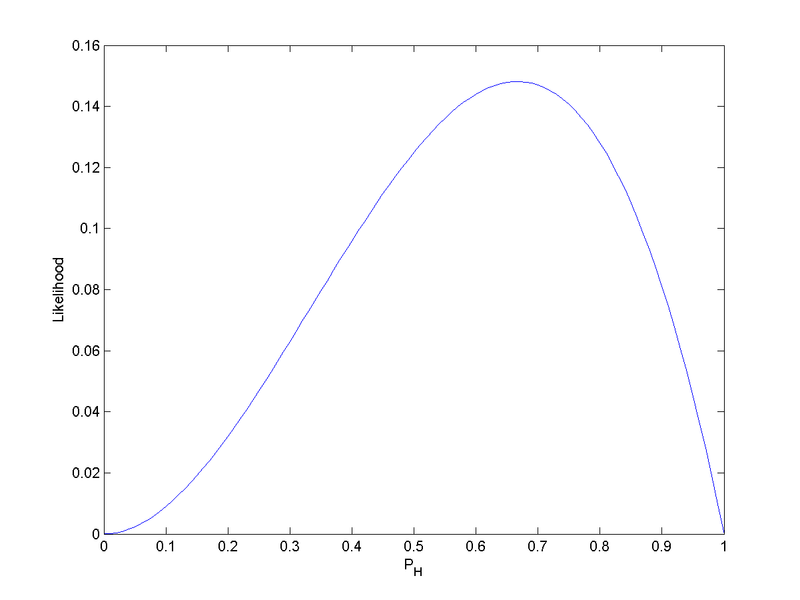
MLE

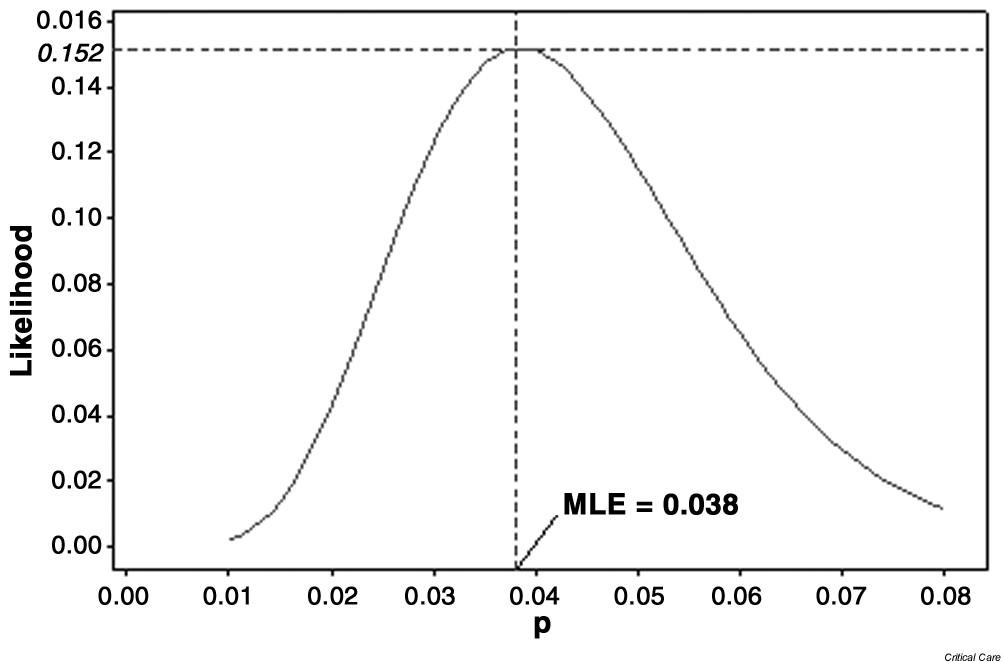
Ways to get MLE

• Calculus - maximize the function.
• Numeric deterministic optimization (Fisher scoring, Newton-Raphson-like, grid search).
• Numeric stochastic optimization (Gibbs, MCMC, HMC).
• Combinations of deterministic and stochastic optimization (simulated annealing).

Fisher scoring

Define log-likelihood, score, and Fisher information function: $$l\left(\theta \given y \right) = log f_\theta(y), \rr{ } S(\theta) = \frac{\partial}{\partial \theta}l\left( \theta \given y\right)$$

$$I\left( \theta \right) = E_y\left[-\frac{\partial^2}{\partial\theta^2}l(\theta \given y)\right]$$

1. Initialize at \\( \theta_0 = \rr{some value} \\).
2. \\( \theta_{i+1} = \theta_i + I^{-1}\left( \theta \right) S \left( \theta_i \right)\\).

Newton-Raphson

1. Initialize at \\( \theta_0 = \rr{some value} \\).
2. \\( \theta_{i+1} = \theta_i - S'^{-1}\left( \theta \right) S \left( \theta_i \right)\\).

There are implementations in R such as optim that perform this numerically given the function \\( S \\).

Hill climbing?

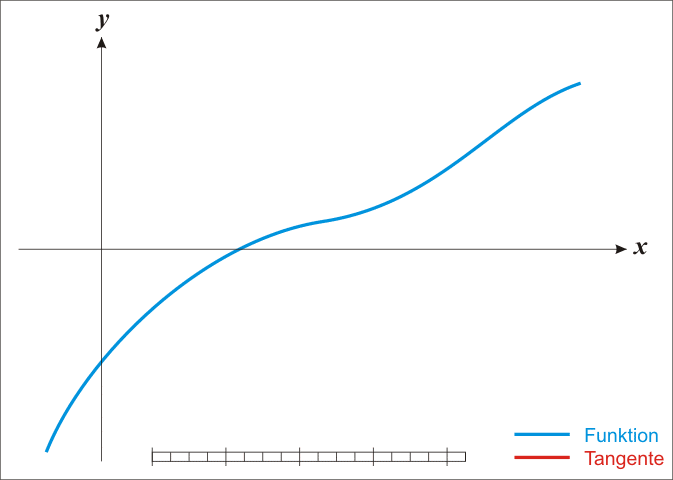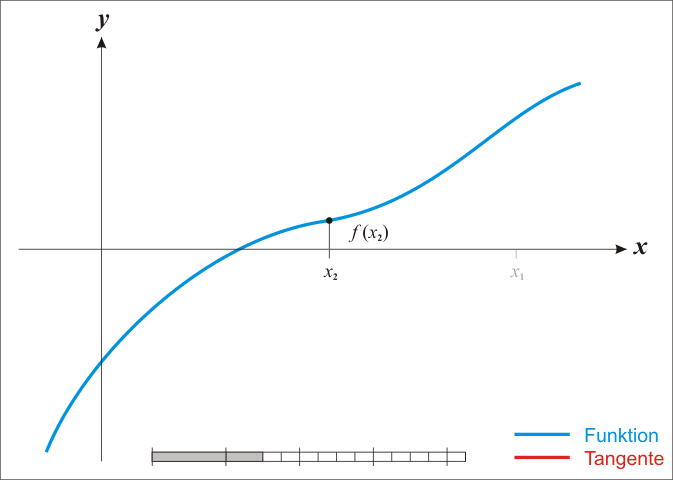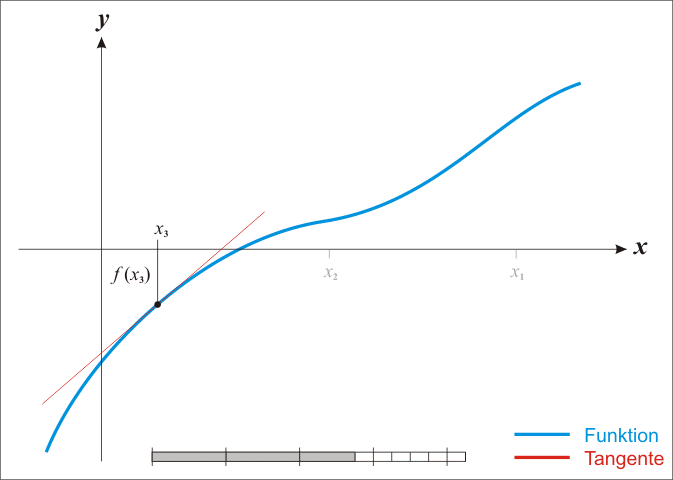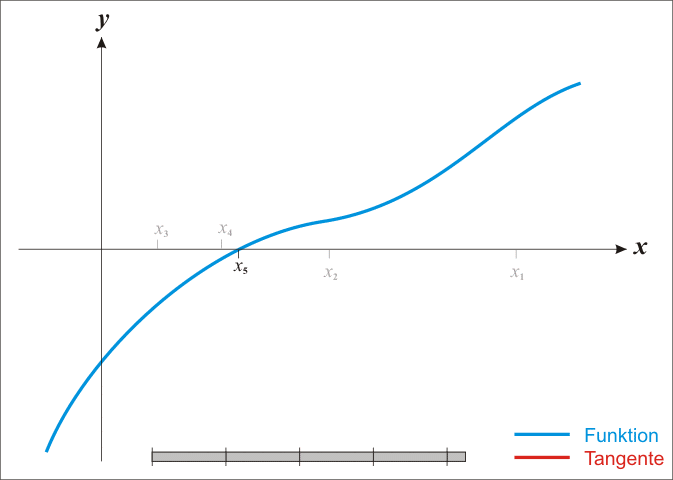
Exponential model

$$f_\lambda(y) = \lambda e^{-\lambda y}$$

$$l\left( \lambda \given y\right) = log\lambda - \lambda y, \rr{ } S(\lambda) = \frac{1}{\lambda} - y, \rr{ } I(\lambda) = \frac{1}{\lambda^2}$$

• Observed and expected information functions equal.
• F-S: \\( \lambda_{i+1} = \lambda_i + \lambda_i^2 \cdot \left( \frac{1}{\lambda_1} - y\right) \\)
• N-R: \\( \lambda_{i+1} = \lambda_i + \lambda_i^2 \cdot \left( \frac{1}{\lambda_1} - y\right) \\)

Computing complexity for F-S and N-R

• Depends on score and information calculation.

Grid search

• Similar to plotting the likelihood function/surface.
• Computing complexity grows exponentially with dimension.

After we get MLE

• Construct 95% uncertainty interval around \\( \hat{\theta}_{\rr{mle}} \\) with $$\hat{\theta}_{\rr{mle}} \pm 1.96 \cdot \rr{SE}\left( \hat{\theta}_{\rr{mle}}\right)$$
• This obviously assumes Normality around the true parameter value.

Alternatives to MLE

• MLE is a point estimation technique that assumes the likelihood function is a bellcurve.
• Full MCMC algorithms do not do that, and may result in better estimation.

Quality control

Regardless of the procedure, verify its numeric properties:

• Numeric stability.
• Interval coverage frequency.
• This is distinct from PPC and CV.

Interval coverage

Simulate from the model many times, fit the model on the generated data, calculate the 95% Confidence Interval around the estimator, and check how frequently it captures the true value of the parameter.

• Helps identify the ideal case sample size necessary for log-likelihood Normality.

Coverage rate

• If MLE assumptions hold, should be close to 95%.
• Otherwise, departure from approx. Normality (small sample size, too many nuisance parameters, nonidentifiability, multimodality)

Numeric stability

• A quicker way to diagnose a procedure.
• Generate and fit the model on data from truth, should recover the truth back.
• Is a "subset" of the interval coverage rate check.

Computing workhorse

• Odyssey, the FAS supercomputer.

"Research Computing provides faculty and researchers with the tools they need to take on large-scale computing challenges. Odyssey, Harvard’s largest supercomputer, offers users over 2.5 Petabytes of raw storage, more than 17,000 processing cores, and numerous software modules and applications."

Sample Odyssey bash script

# Stat 221
# Problem set 2 answer 1d
# bash job execution script
 
# answer prefix - please do not change
answer="answer1d"
pset="\"Problem set 2\""
 
# set the student name
student="\"First name Last name\""
# set working directory - important!
wd="~/stat221/pset2"
 
# record the email of the user
email="fasusername@fas.harvard.edu"
 
# define the queue we'd like to use
queue="short_serial"
 
# define other arguments
fn="answer1d-odyssey-student"
infile="data/answer1c-INDEX.Rdata"
niter=4
msg="Submitting the optim vs. Fisher scoring summarization script"
 
file="../bsub/$answer.bsub"
 
# very important to remember to list all your arguments here
line="R --no-save --args answer $answer wd $wd student $student "
line+="pset $pset infile $infile niter $niter "
line+="< $fn.R 1> $wd/test/jobreports/$fn.out "
line+="2> $wd/test/jobreports/$fn.err"
echo "$line" >> ${file}
# start the job 
echo "$msg."
bsub < ${file}

Announcements

• T-shirt competition winner, Twitter.

Resources

• Slides nesterko.com/lectures/stat221-2012/lecture7
• Class website theory.info/harvardstat221
• Class Piazza piazza.com/class#spring2013/stat221
• Class Twitter twitter.com/harvardstat221

Final slide

• Next lecture: simulated annealing, Gibbs, MCMC, more on distributed computing and Odyssey