The final lecture

Stat 221, Lecture 25

@snesterko

Roadmap

What the class was about
Class material recap
- Theoretical material
- Computing
- Visualization
- What's your favorite?
Student creations
Where can we go from here?

The class was about the full data analysis workflow

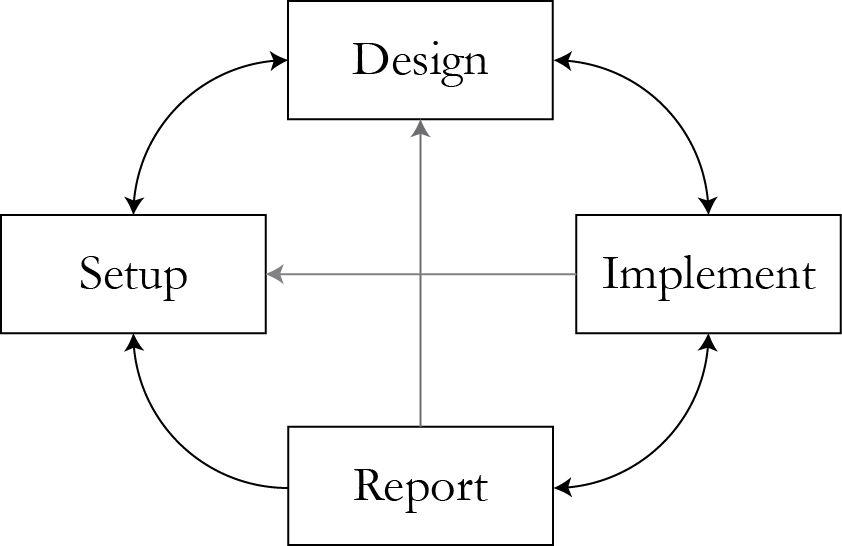
What we went through

Theoretical material

Topics we have explored:

Classic point estimation: MLE, Fisher scoring
Point estimation with missing data: EM+
Full-posterior inference: MCMC, HMC, Parallel Tempering, Equi-Energy Sampler
Decisions based on inferred system parameters
A structured approach to interactive visualization

Observed Fisher Information puzzle

Mysteries of classic MLE estimation

Reparametrization brings more information from the same data
Perfect models have a unimodal likelihood
- By consequence, imperfect models misbehave: the likelihood is not unimodal, log-likelihood does not look Normal

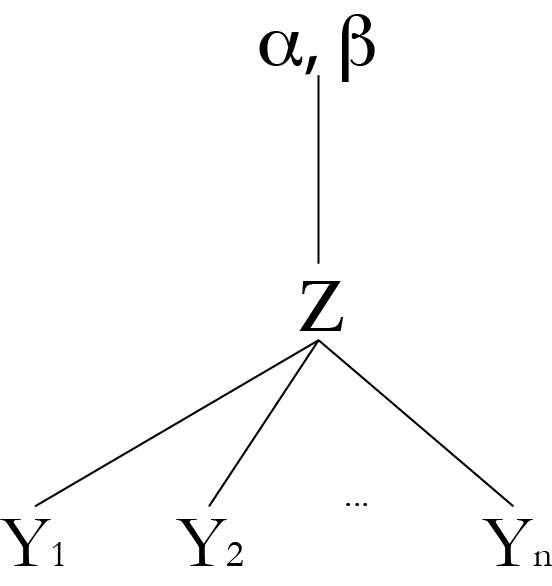
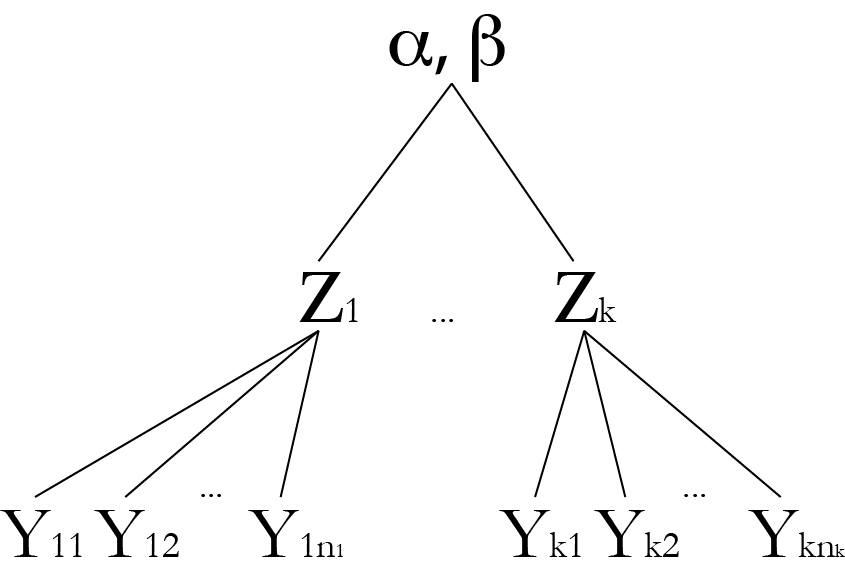
Modeling with missing data and latent variables - replication is crucial!

Much better with replication

EM: mystery of the \$ Q \$ function

$$Q\left( \theta | \theta^{(t)} \right) = \int l(\theta | y) f( Y_{\rr{mis}}| Y_{\rr{obs}}, \theta = \theta^{(t)}) dY_{\rr{mis}}$$

By Jensen's $$\begin{align} l( \theta^{(t+1)} | & Y_{\rr{obs}}) - l( \theta^{(t)} | Y_{\rr{obs}}) = \\ & [Q( \theta^{(t+1)} | Y_{\rr{obs}}) - Q( \theta^{(t)} | Y_{\rr{obs}})] \\ & - [H( \theta^{(t+1)} | Y_{\rr{obs}}) - H( \theta^{(t)} | Y_{\rr{obs}})] \geq 0\end{align}$$

Puzzle: can the \$ Q \$ function be used to stop bad EM early?

Intro hacker level with EM: data augmentation

Introducing missing data when it's not there: simple \$ \rr{Normal} + \chi^2_n =t_n \$ mixture example.
Down the rabbit hole: PX-EM
- Why did we stop there?
- Data augmentation/parameter space expansion = improved numerical properties of algorithms at the expense of harder implementation

MCMC for when log-likelihood isn't Normal

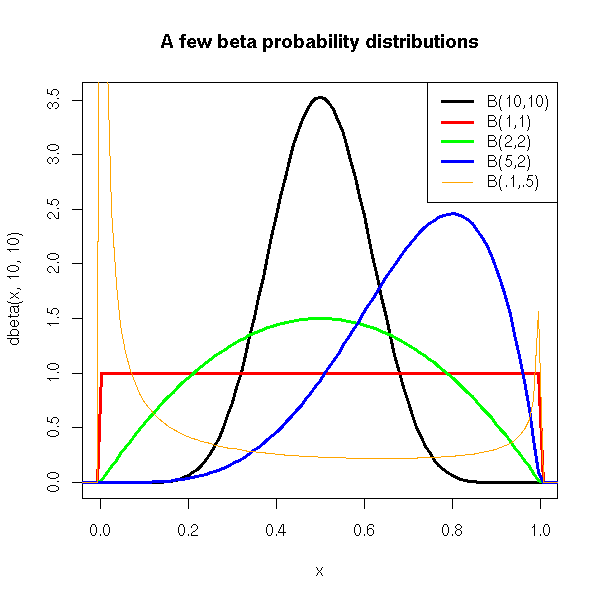
Going deeper: imperfect models, multimodal posteriors

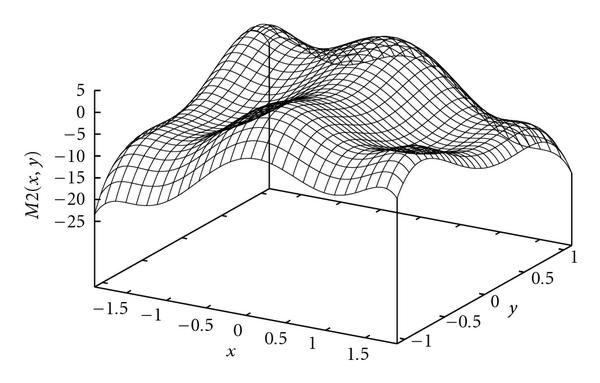
"Strictly better than Metropolis" - HMC

Hamiltonian (Hybrid) Monte Carlo, a so-called "derivative-based" MCMC technique.
Performs very well for differentiable energy functions (densities).
Generic implementation, but with a twist
- The gradient needs to be evaluated up to 10-20 times per single MCMC iteration. Its implementation should be fast enough.

HMC mechanics

HMC is great for fast convergence, but only for something like this

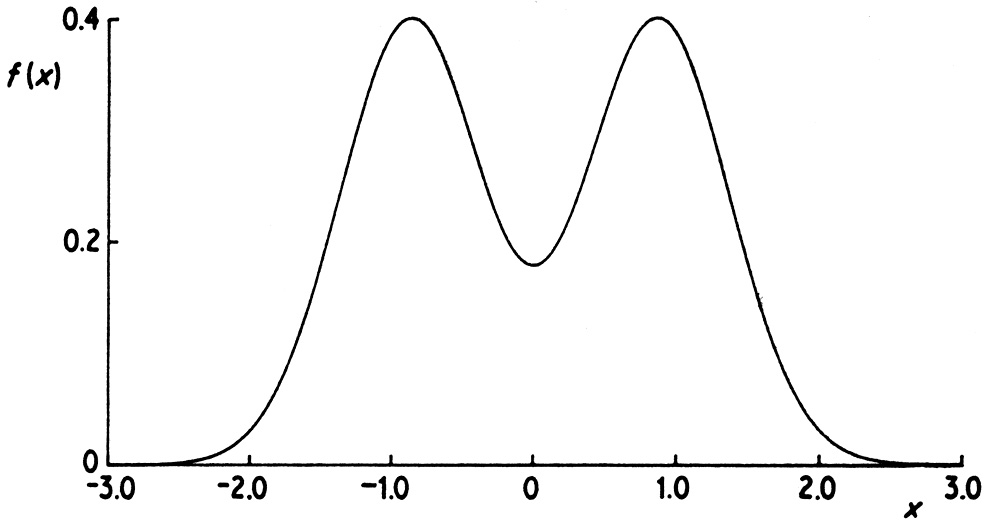
Going beyond HMC: Parallel Tempering

Running chains in parallel, swapping draws between them in order to explore the space better.
Can be used with any MCMC strategy inside each chain: Metropolis, Metropolis-Hastings, Hamiltonian Monte Carlo, Slice Sampler etc.
Works better than any single chain with the same local jump, but takes time and effort to implement, computing infrastructure to execute (MPI, cloud).

Parallel Tempering mechanics

Further questions with PT

What are the optimal setting of PT?
Do non-blocking MPI designs for PT really have a positive affect?
Are PT-like algorithms really the future of statistical computing?

Making PT obsolete - the EE sampler

The Equi-Energy Sampler makes uniform equi-energy proposals from the pools of previously visited states with similar energy values. This allows to directly make MCMC jumps between the modes that are potentially far apart.
Superior performance of the EE sampler comes at the price of harder technical implementation, large required memory storage.

EE Sampler illustrated

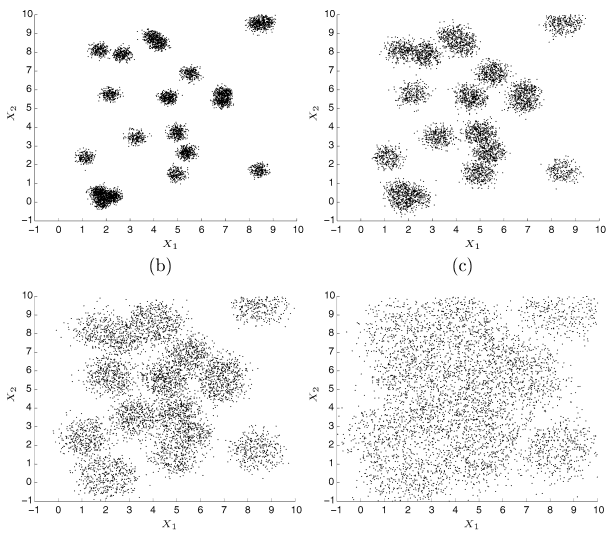
EE sampler vs PT sampler

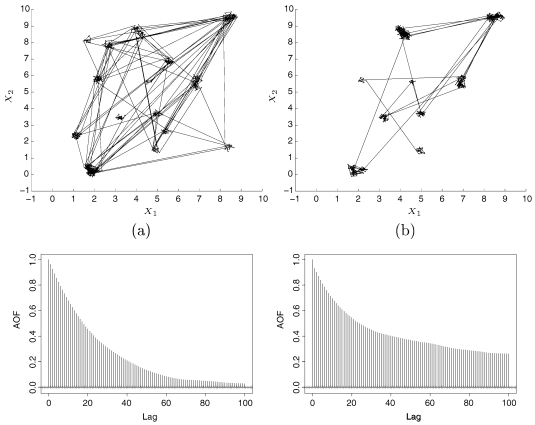
Open research with the EE sampler

Can we define continuous energies for each temperature values so that we can use HMC with EE?
The EE sampler takes us to the limit: is it more an optimization algorithm or more an inference algorithm. Specifically, highly multidimensional statistical models don't make sense (or do they?).

Having inferred system parameters, need to decide

Desicion Theory is not well adapted to real world decision problems that actual movers and shakers need to make based on data-driven systems. $$ \int C(\theta, \delta(X)) p(\theta \given R, X) d \theta$$
Defining the right cost function, connecting to Response Surface methods, RCM - open research areas.

Computing!

Can't live with it, can't live without it
Several themes in R programming
- Vectorization
- Code abstraction
- Cloud computing
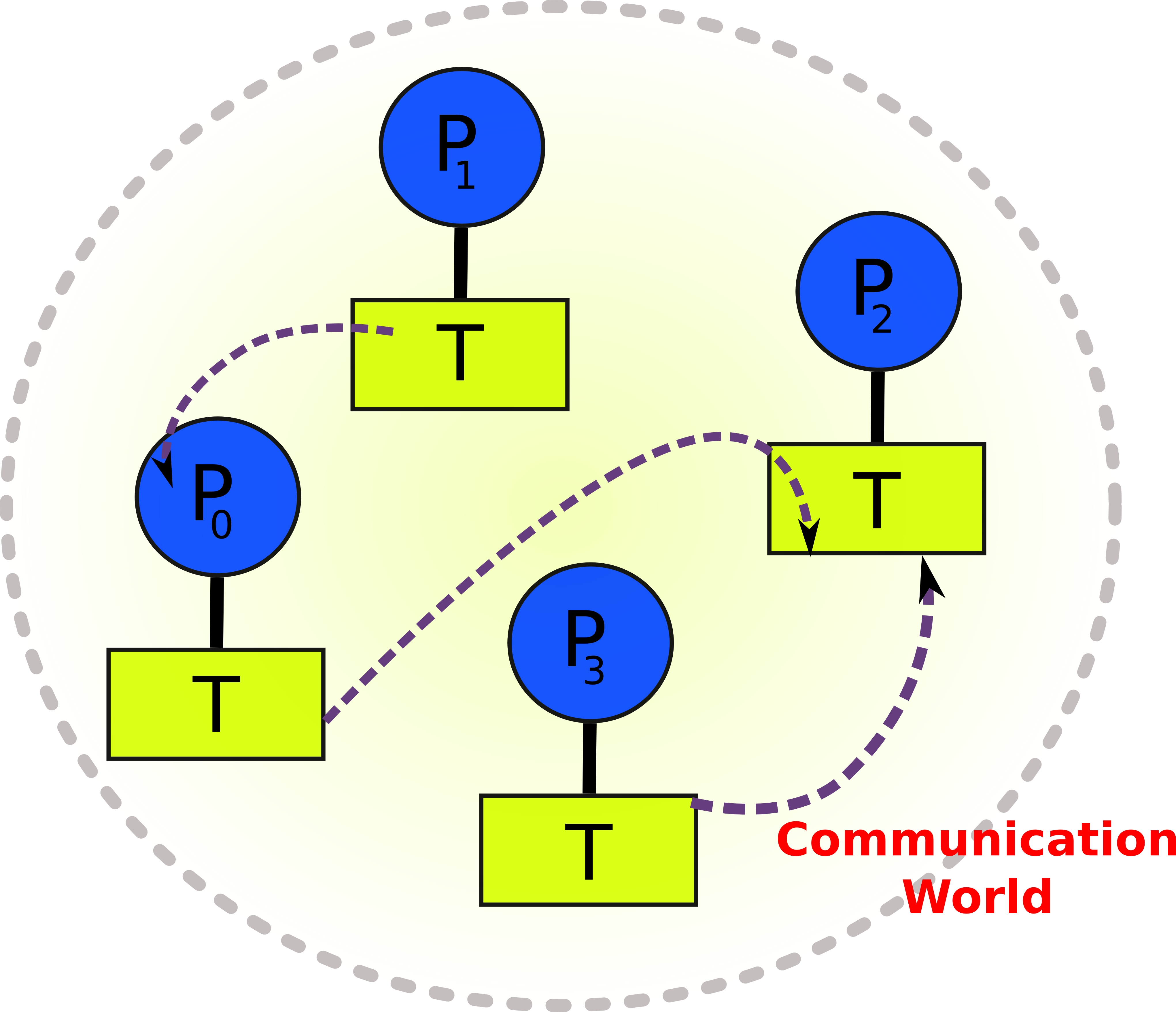
- Parallel computing with MPI+friends
Are we expert R programmers now?

Vectorization

time1 <- proc.time()
res1 <- sapply(1:1000000, exp)
time2 <- proc.time()
time2 - time1
## user system elapsed
## 6.321 0.146 6.429
 
time1 <- proc.time()
res2 <- exp(1:1000000)
time2 <- proc.time()
time2 - time1
## user system elapsed
## 0.022 0.016 0.051
all(res1 == res2)
## [1] TRUE

MPI

Visualization

What we've learned

The impact of interactive experiences
Technical interactive visualization
Tools how to make it with d3js
Structuring the perception, evaluation of interactive experiences
Technical features of visualization

Classifying visualizations

By goal
- Engage
- Provoke thinking
- Make them pay you
- Other
By audience
- General audience
- Scientific audience
- Other
By type

Visualization type

Comparison is important

Another one

Building analogy (Steven Wittens)

Creating interactive experiences has become easier than ever

SVG standard development
HTML5
WebGL
Cinder
Not so bad to learn and use!

Class visualization tools

plot(1~1)
## or
library(ggplot2)
p <- ggplot(data.frame(x = 1, y = 1), aes(x, y))
p + geom_point()

d3js

// initialize the SVG container
var con = d3.select("#" + container)
            .insert("div", ":first-child")
            .attr('class', 'ivcont');
// add visualization title
con.append("h2").html(title);

Student work - great!

Where can we go from here?

Anywhere*

*Class material is universal and can help be effective when dealing with data at the highest level of complexity both technically and conceptually.

Announcements

Final project write-up/code submissions due tomorrow 11:59pm
Final project presentations Wednesday May 8 at 1-4:12pm - everyone is expected to attend