Introduction to visualization+modeling+computing (VMC) I
Stat 221, Lecture 2
More on final project
- Team assignment details.
- Descriptions released approx. February 2.
Student questions, administrative
- Can submit visualizations to class website! Good for participation.
- What is good style of code?
- Homework previews.
- Time commitment to problem sets.
- d3js support possibilities (online tutorials, workshop, TF)
- T-shirt competition clarified.
Modeling
Many areas apply modeling
- Statistics
- Computer science
- Ecomonics
- Physics
- Biology
- others
Statistical models
- Close to physics, chemistry, biology etc.
- Defining trait - distributional assumptions on noise.
- Similar to Computer Science when no clear intuition driving the process can be found.
Main ingredients
Response, data, noise, and parameters:$$\begin{align} \rr{response} &= f(\rr{data}, \rr{noise})\\ Y &= f_{\theta}(X, \epsilon) \end{align}$$

Ways to write it down
Representation:$$\begin{align}Y &= f_{\theta}(X, \epsilon) \rr{ or} \\ Y &\sim f_{\theta}(X, \epsilon)\end{align}$$
Graphical or generative :


Representation examples
Linear regression:$$\vec{Y} \sim \mathbf{X}\vec{\beta} + \vec{\epsilon}, \rr{ } \vec{\epsilon} \sim N\left(0, \sigma^2\mathbf{I}\right)$$
Anchor Process: $$\begin{align} Y_i \given Y_{r(i)} & \sim N \left(\rho Y_{r(i)} + (1 - \rho) \mu, (1 - \rho^2) \sigma^2 \right), \\Y_i & \sim N\left( \mu, \sigma^2 \right) \rr{ if } r(i)\rr{ doesn't exist}\end{align}$$
How do you design these?
- Translate scientific/expert intuition into mathematical statements.
- Follow the quantitative analysis workflow.
Models as stories
- Each model tell a story.
- Let's tell a story - class activity.
The workflow
Iterate between the stages:
- Initialize: talk to collaborator/client, get the data, understand the question of interest.
- Design: an analytic method for a solution, evaluate its properties and assumptions.
- Implement: a working, practical computing solution to perform the designed procedure.
- Communicate: the findings, help understand and interpret them. Advise on the method's applicability in case of repeated use.
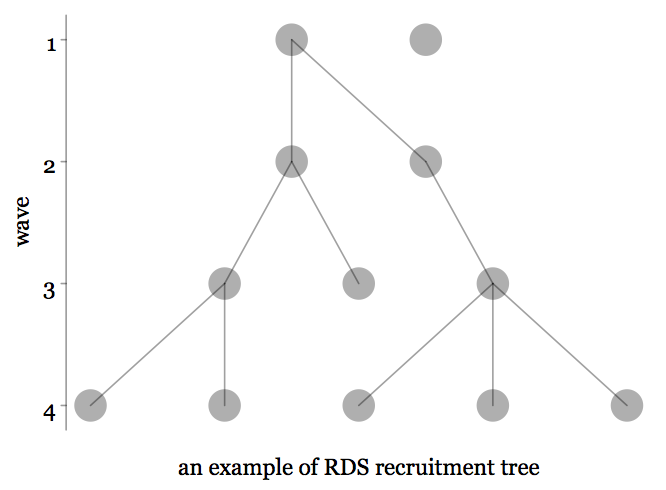
Case study: RDS
- Respondent-Driven Systems/Sampling
- Respondents follow their social network to recruit peers to achieve a common goal.
- Public health agencies are interested in estimating population average income, illness status etc.
How RDS looks
The first guess
The first guess for the model is $$Y_i \mathop{\sim}^{\rr{iid}} N\left( \mu, \sigma^2\right)$$
Yields the classic vanilla estimator $$\hat{\mu} = \bar{Y}$$
with liberal (tight) confidence bounds.
Almost no computation is needed for this model.
A problem
- The model is unbiased, but
- The naive 95% confidence interval has coverage of around 20% in case of homophily.
- How do we enhance our model to keep the unbiasedness, but achieve the right coverage rate for uncertainty intervals?
An approach to solve it
- Understand the system better.
- Build the intuition about system mechanics into our estimation model.
- Hope that our intuition and the way we've postulated it are good enough.
An RDS sample
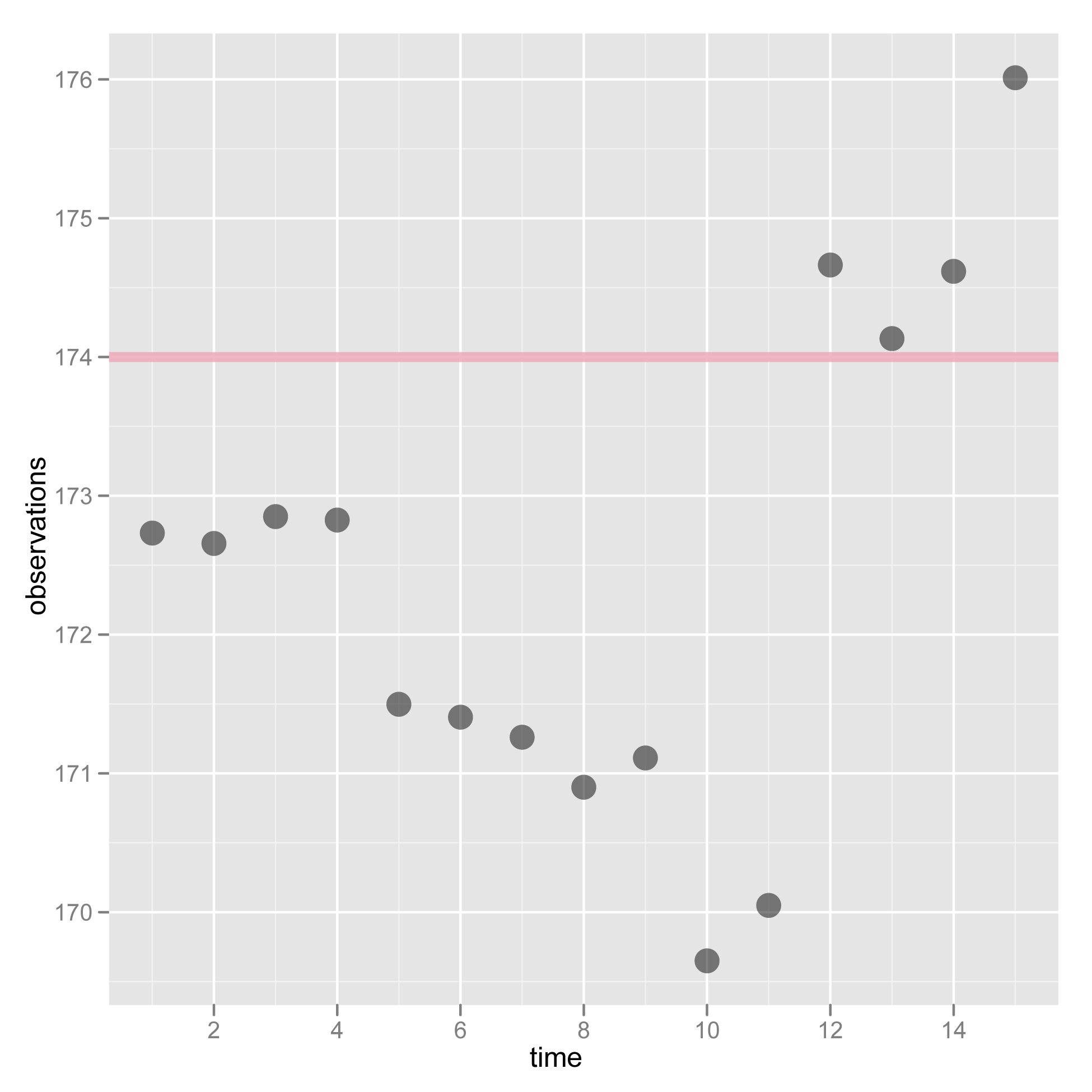
Distribution+network (with homophily)
Two variants of population networks
RDS with homophily
Anchor Process model
Model statement: $$\begin{align} Y_i \given Y_{r(i)} & \sim N \left(\rho Y_{r(i)} + (1 - \rho) \mu, (1 - \rho^2) \sigma^2 \right), \\Y_i & \sim N\left( \mu, \sigma^2 \right) \rr{ if } r(i)\rr{ doesn't exist}\end{align}$$
- \\( \{ \rho, \mu, \sigma^2 \} \\) is the parameter set
- \\( r(i) \\) is the index of referrer of respondent \\( i \\).
- \\( Y_i \\) is the observation of respondent \\( i \\).
- Needs more involved computation - there is no closed-form solution for \\( \hat{\mu} \\).
AP model performance
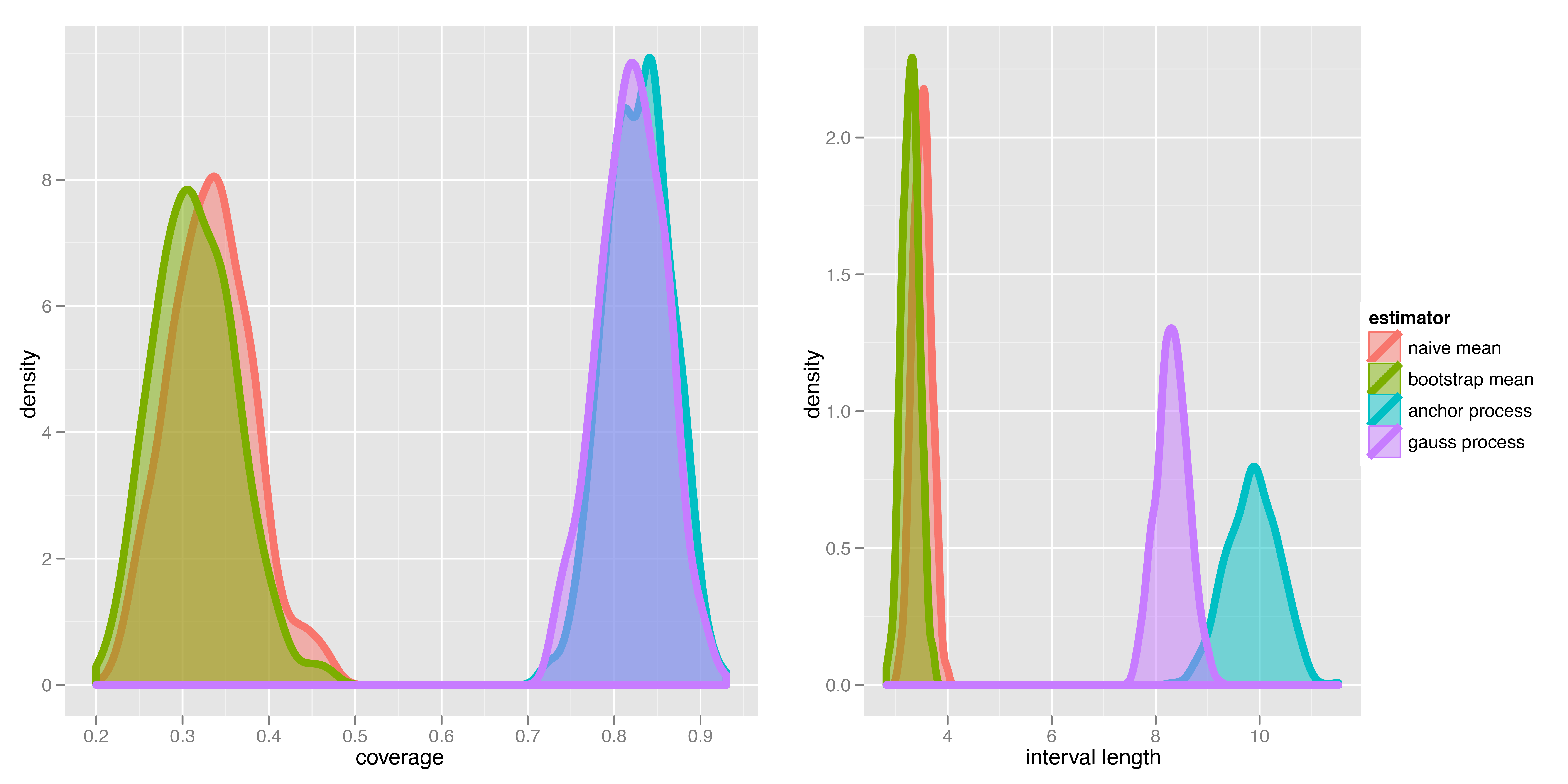
AP model simulation
What drives the process?
- The question to be answered a.k.a. the estimand.
- Developing the intuition of how things work.
- Translating the intuition into models, evaluating their properties.
- Being able to fit/compute with these models.
- Reporting the results.
- Looping back.
Announcements
- Final project proposals available soon - check email and course Twitter!
- Odyssey access, ask your TF for clarifications.
- Free T-shirt competitions start now!


Resources
- Slides nesterko.com/lectures/stat221-2012/lecture2
- Class website theory.info/harvardstat221
- Class Piazza piazza.com/class#spring2013/stat221
- Class Twitter twitter.com/harvardstat221
Final slide
- Next lecture: Introduction to data Visualization + statistical Modeling + Computing (VMC) II
- Don't hesitate to talk to course staff about the class and your specific needs.