Parallel Tempering

Stat 221, Lecture 18

@snesterko

Roadmap

  • Multimodality as a challenge for MCMC
  • MCMC diagnostics
  • Parallel Tempering algorithm
  • General structure of a PT program

Where we are

Multimodality

  • It is a very common feature in likelihood/posterior surfaces.
  • What causes it?
    • Non-identifiabilities.
    • Overfitting.
    • Multiple likely parameter configurations.
  • To extract all information from the posterior surface, need to be able to effectively sample from it.

Example

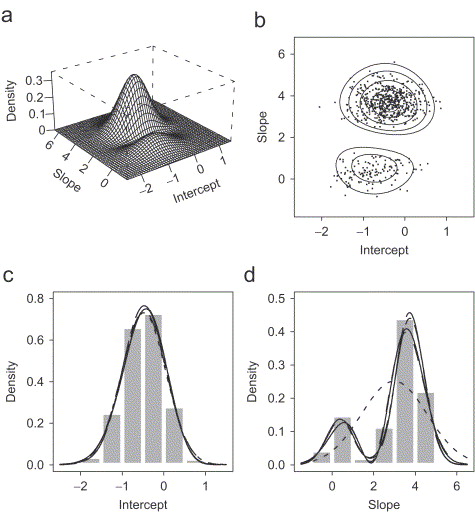
Now more complex

  • Latent class regression as in the problem set: \\( 24 \times \rr{nclasses} \\) regression parameters.
  • Protein folding.
  • Any complex system + imperfect modeling.

Areas of open research

  • Overfitting.
  • Model selection.
  • Questions:
    • How to disambiguate natural versus modeler-imposed multimodality?
    • What metrics should we use to know that a given model is sufficient?
    • In a world with perfect modelers, would MLE estimation suffice?

But for now

  • Need to be able to sample from posterior surfaces to get an answer.

Strategies

  • "Running your MCMC long enough"
  • Start with random points, and:
    • MCMC
    • Point estimation + curvature
  • Simulated Tempering
  • Parallel Tempering
  • Equi-energy Sampler

Why naive MCMC isn't good

  • We don't know how long is "long enough". In addition to visual inspection, there are several convergence diagnostics:
    • Gelman-Rubin
    • Geweke
    • Raftery-Lewis
  • Often, need to run prohibitively long to achieve acceptable mixing.

The Geweke diagnostic

  • Run the MCMC chain for some time.
  • Consider two non-overlapping parts of the chain.
  • Run a difference in means test adjusting for autocorrelation.
    > geweke.diag(mh.draws)
Fraction in 1st window = 0.1
Fraction in 2nd window = 0.5
var1   var2
0.6149 0.1035
  • Gelman-Rubin diagnostic is slightly more involved.

Gelman-Rubin diagnostic

  • First, need to run multiple chains, for example, \\( m \\) chains.
  • Compute within-chain variance estimator for parameter \\( \theta \\) $$W = {1 \over m } \sum_{j=1}^m s_j^2$$ with $$s_j^2 = {1 \over n-1} \sum_{i=1}^n(\theta_{ij} - \bar{\theta}_{j})^2$$
  • Likely, \\( W \\) underestimates the true variance.

Across chains

  • Compute between chain variance estimate $$B = { n \over m-1} \sum_{j=1}^m (\bar{\theta}_j - \bar{\bar{\theta}})^2$$ with $$\bar{\bar{\theta}} = {1 \over m} \sum_{j=1}^m \bar{\theta}_j$$
  • This is variance of each chain average multimplied by \\( n \\) - the number of draws in each chain (why?)

Viariance of stationary distribution

  • Based on \\( W \\) and \\( B \\), estimate variance of stationary distribution $$\hat{\rr{Var}} \theta = \left( 1 - {1 \over n}\right) W + {1 \over n} B$$
  • Because of overdispersion in starting values, this is likely to overestimate the true variance.
  • The estimator is unbiased if starting values come from the stationary distribution.

Scale reduction factor

Compute $$\hat{R} = \sqrt{\hat{\rr{Var}} \theta \over W}$$

If \\( \hat{R} \\) is high, we should run chains longer to improve convergence to the stationary distribution.

  • For this diagnostic, need to run multiple chains.
    • Which diagnostic is better - Geweke or Gelman-Rubin?

Gelman-Rubin diagnostic code

mh.draws1 <- mcmc(NormalMHExample(n.sim = 5000, n.burnin = 0))
mh.draws2 <- mcmc(NormalMHExample(n.sim = 5000, n.burnin = 0))
mh.draws3 <- mcmc(NormalMHExample(n.sim = 5000, n.burnin = 0))
mh.draws4 <- mcmc(NormalMHExample(n.sim = 5000, n.burnin = 0))
mh.draws5 <- mcmc(NormalMHExample(n.sim = 5000, n.burnin = 0))
mh.list <- mcmc.list(list(mh.draws1, mh.draws2, mh.draws3, mh.draws4,
+ mh.draws5))
gelman.diag(mh.list)

Use

gelman.plot(mh.list)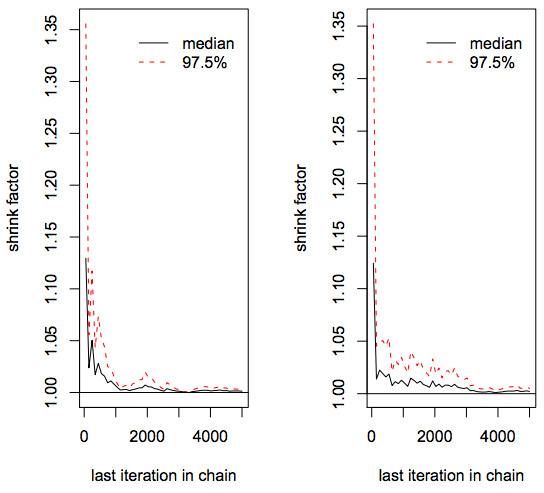

Starting with random points

  • Very practical.
  • But there isn't much guarantee that we explore the whole space.
  • A good starting point for a more substantial algorithm.

Simulated Tempering

  • Data augmentation! Ideas borrowed from physics.
  • Every density function can be rewritten in this way: $$f(x) = e^{-(-\rr{log}f(x))}$$
  • Define energy \\( E(x) = -\rr{log}f(x)\\)
  • Aim to simulate from $$f(x, T) = e^{- {1 \over T} E(x)}$$
  • \\( T \in \{ T_1, T_2, \ldots, T_m\}\\) - pre-defined set of temperature levels (presumably including temperature 1).

Properties

  • Sample from the joint temperature-parameter space.
  • Only use the draws from the parameter space with temperature 1.
  • Will we ever converge in the temperature space?
  • Can this algorithm be parallelized?

Parallel Tempering

  • Aims to use the ideas of simulated tempering.
  • Amenable to (designed for) parallelization.
  • Idea: run chains at different temperatures in parallel, and "swap" parameter values between them once in a while.
  • Goal: improve mixing at temperature 1.

Definitions

Define composite system $$\Pi (X) = \prod_{i=1}^N {e^{- \beta_i E(x_i)} \over Z(T_i)}$$

with \\( \beta_i = {1 \over T_i }\\) and \\( Z(T_i) = \int e^{- \beta_i E(x_i)} dx_i\\).

  • \\( \Pi \\) reduces to \\( f \\) if \\( T_i = 1 \\).
  • At each iteration \\( t \\), construct a Markov Chain to sample from \\( E(\cdot) \\) at \\(T_i\\) for each \\(i \\).

Putting into context

Problem set 5 example

$$\begin{align} & \rr{log} p(\vec{Z}_i, B \given C_{ijk} ) = \rr{const} + \\ & \sum_{i=1}^I \left( \sum_{j \in J_i} \sum_{k \in K_{ij}} \left[ \vec{x}_{jk}' B - \rr{log} \sum_{l = 1}^{L_j} e^{ \vec{x}_{jl}' B} \right] \right) \cdot \vec{Z}_i \end{align}$$

Call parameters \\( \theta \\), look at \\( \rr{log}p(\theta \given y) \\).

Define components for Parallel Tempering

  • Energy function \\( E(\theta) = - \rr{log} p(\theta \given y) \\).
  • Set energy levels \\( T = \{ T_1, T_2, \ldots, T_n \} \\)
    • What is the optimal temperature ladder?
  • Composite system $$\Pi (\theta) \propto \prod_{i=1}^n \rr{exp}\left\{-{1\over T_i} E(\theta_i)\right\}$$

The algorithm

initialize N temperatures x_1, ..., x_N
initialize N replicas x_1, ..., x_N
repeat {
  sample a new point x_i for each replica i
  with probability theta {
    sample an integer j from U[1, N-1]
    attempt a swap between replicas j and j + 1
  }
}

Parallel Tempering

Intuition behind PT

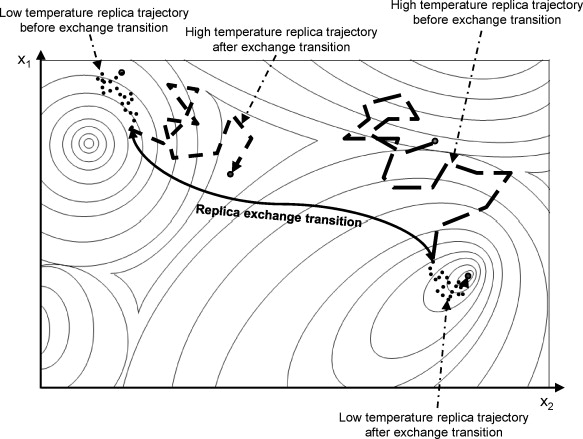
PT performance

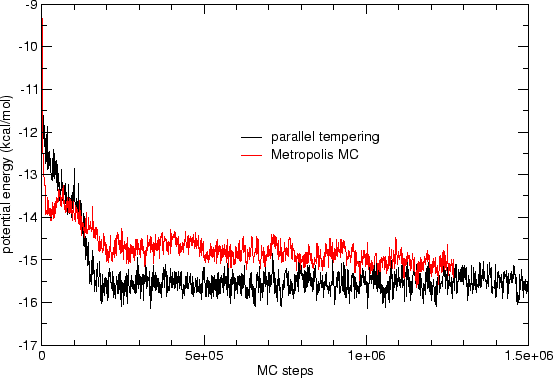
Acceptance probabilities

  • Local moves \\(w_{\rr{local}} (x_i \rightarrow x_i') = e^{-\beta_i \Delta_i E} = e^{-\beta_i (E(x_i') - E(x_i))}\\)
  • Replica exchange across chains

$$\begin{align} &P_{\rr{replica}} (x_i \leftrightarrow x_{i+1}) = \\ & P( x_1, \ldots, x_{i+1}, x_i, \ldots, x_N \given \ldots, x_i, x_{i+1}, \ldots) \\ & = \rr{min} \left( 1, {\Pi(x_1, \ldots, x_{i+1}, x_i, \ldots, x_N) \over \Pi(x_1, \ldots, x_i, x_{i+1}, \ldots, x_N) }\right)\\ & = \rr{min} \left( 1, e^{(\beta_i - \beta_{i+1})(E(x_i) - E(x_{i+1}))}\right)\end{align}$$

How to make it parallel

  • Run everything on one node (multicore vs no parallelization).
  • Can tell worker nodes to run chains.
  • Handling replica exchange communication (main thing):
    • All through the master node.
    • Allow maximum inter-worker communication, independent of the master.
  • Pros and cons of each method?

Blocking vs non-blocking design

  • Blocking design is when your parallel computing system sits idle waiting for something to occur.
  • Non-blocking design is when we minimize unnecessary wait times so that the nodes do what they are supposed to do (compute) and don't sit idle.

Non-blocking design

  • Want to minimize inter-node communication
    • Running identical random number streams on workers.
    • Communicate directly with another worker and not through master.

PT random number streams

  • For this, need to be able to initialize random number streams at the same value and send them to workers.

Random number generation

  • Reference: "Parallel Random Number Generation in C++ and R Using RngStream" by Andrew Karl, Randy Eubank, and Dennis Young
  • Use sequence:

$$\begin{align}x_{1,n} = &(1403580 \cdot x_{1,n−2}−810728\cdot x_{1,n−3}) \\ & \rr{mod } 4294967087 \\ x_{2,n} = & (527612 \cdot x_{2,n−1}−1370589 \cdot x_{2,n−3}) \\ & \rr{mod } 4294944443 \end{align}$$

Get uniform RV

The "uniform" random draw is \\( u_n \\):

$$\begin{align} z_n & = (x_{1,n} − x_{2,n} ) \rr{ mod } 4294967087 \\ u_n & = \begin{cases} z_n/4294967088 & \rr{if } z_n > 0 \\ 4294967087/4294967088 & \rr{if } z_n = 0 \end{cases}\end{align}$$

Parallel Tempering program structure

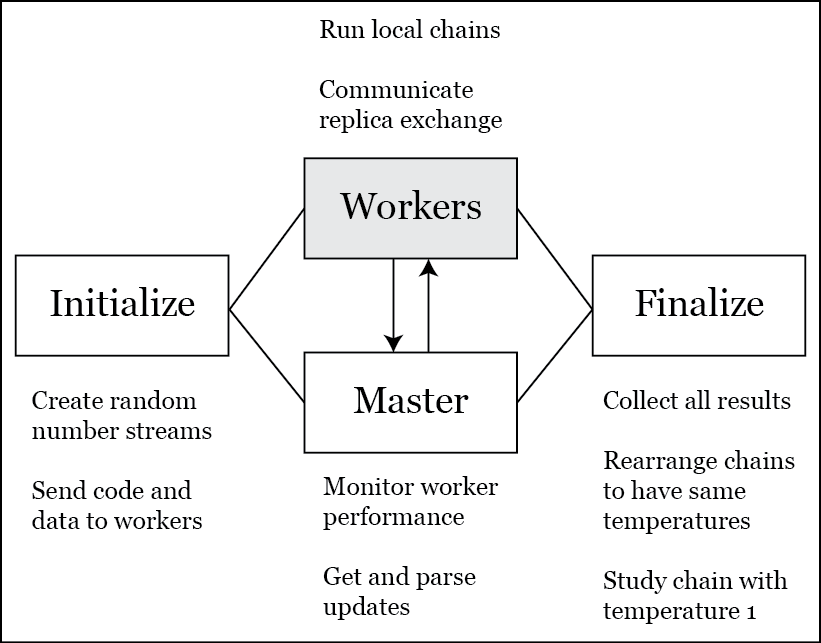
Given target density, the PT algorithm is almost generic

  • The only component that's not generic is the within-chain sampling algorithm.
    • What MCMC algorithms could we use for the within-chain sampling?
  • This means we can have a generic implementation that we can vary from problem to problem.

Announcements

  • Code leaderboard winner for pset 3!
  • Final project second checkpoint.

Resources

Final slide

  • Next lecture: MPI for Parallel Tempering.