Parallel statistical computing
Stat 221, Lecture 17
Where we are
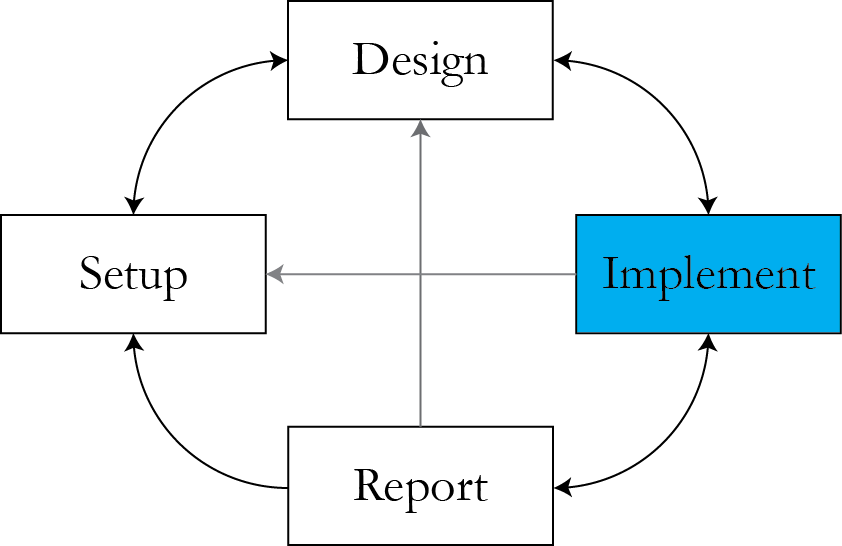
What is parallel computing

Any algorithm
that can be executed by a number of independent workers (possibly, in communication with each other), can be reframed as a parallel computing exercise.
- Likelihood calculation.
- MCMC chains.
- Optimization.
- Data processing.
Parallelization of one of the following types:
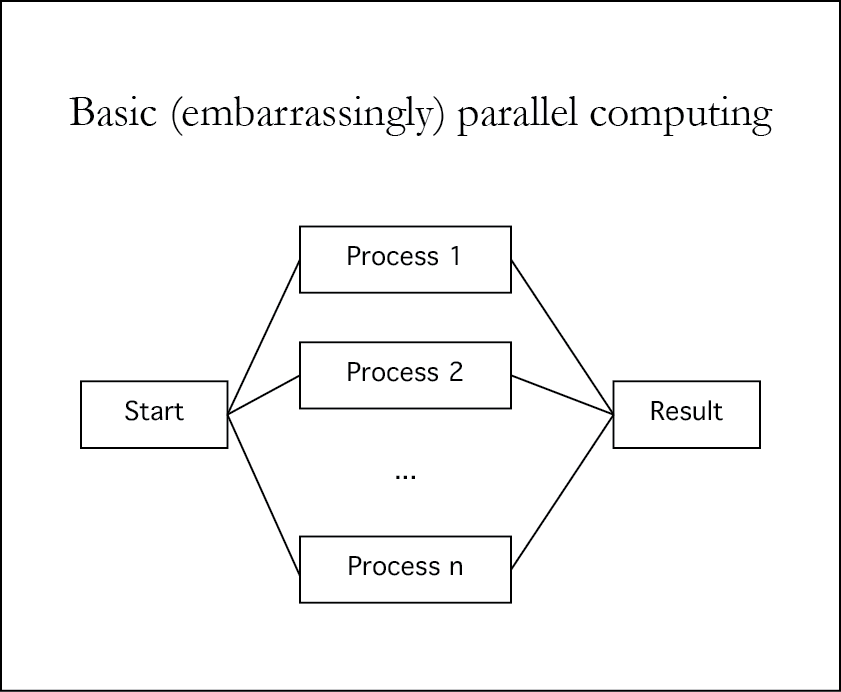
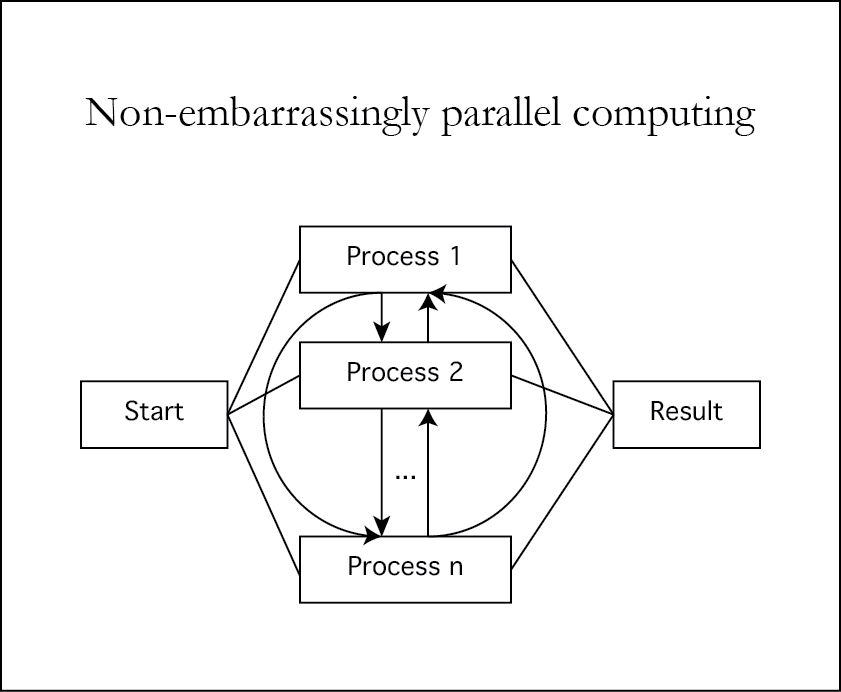
Example: data processing
- In the document authorship example, determining features and calculating feature counts
- In the optimization of marketing campaigns example, preparing data for the fitting procedure and optimization, calculating sufficient statistics
- And so on
Example: likelihood
Document authorship example
- Document authorship \\( \pi_d \sim \rr{Dirichlet}_K(\vec{\alpha},1) \\).
- Data \\( y_{dw} \given \pi_d \sim \rr{Poisson}(\sum_k\mu_{kw}\pi_{dk})\\).
- Author \\( k\\), document \\( d \\), word \\( w \\).
- \\( \pi_{dk} \\) represents the amount of contribution of author \\( k \\) do document \\(d\\).
Likelihood
For document \\( d \\):
$$\begin{align}L(\alpha, \mu, \pi \given y) \propto & \prod_{w=1}^W\left[\left(\sum_k\mu_{kw}\pi_{dk}\right)^{y_{dw}} \right. \\ & \left.\cdot e^{-\left(\sum_k\mu_{kw}\pi_{dk}\right)}\right] \cdot \prod_{k=1}^K \pi_{dk}^{\alpha_k - 1}\end{align}$$
We really want to compute the log-likelihood, however.
Log likelihood
For document \\( d \\):
$$\begin{align}l(\alpha, \mu, \pi & \given y) \propto \sum_{w=1}^W\left[y_{dw}\rr{log}\left(\sum_k\mu_{kw}\pi_{dk}\right)\right. \\ & \left. -\sum_k\mu_{kw}\pi_{dk}\right] + \sum_{k=1}^K (\alpha_k - 1)\rr{log}\pi_{dk}\end{align}$$
This is just for a single document \\( d \\), so can parallelize if we have many documents. How to do that?
Example: optimization
Optimize decision \\( \delta(X) \\) based on inferred parameters
$$ \int C(\theta, \delta(x)) p(\theta \given y, x) d \theta$$
- Good when doing Gaussian mixture approximation.
- Full sampling approach can still be parallelized:
- Parallel tempering
- Approximate methods such as variational inference (careful, approximation!)
Questions that arise
- What is the price for parallelization?
- Specifically, communication speed.
- Implementation difficulty.
- Is it worth it?
Types of parallel computing
- Multithreading
- MPI
- GPU
- Grid computing
Multithreading
MPI
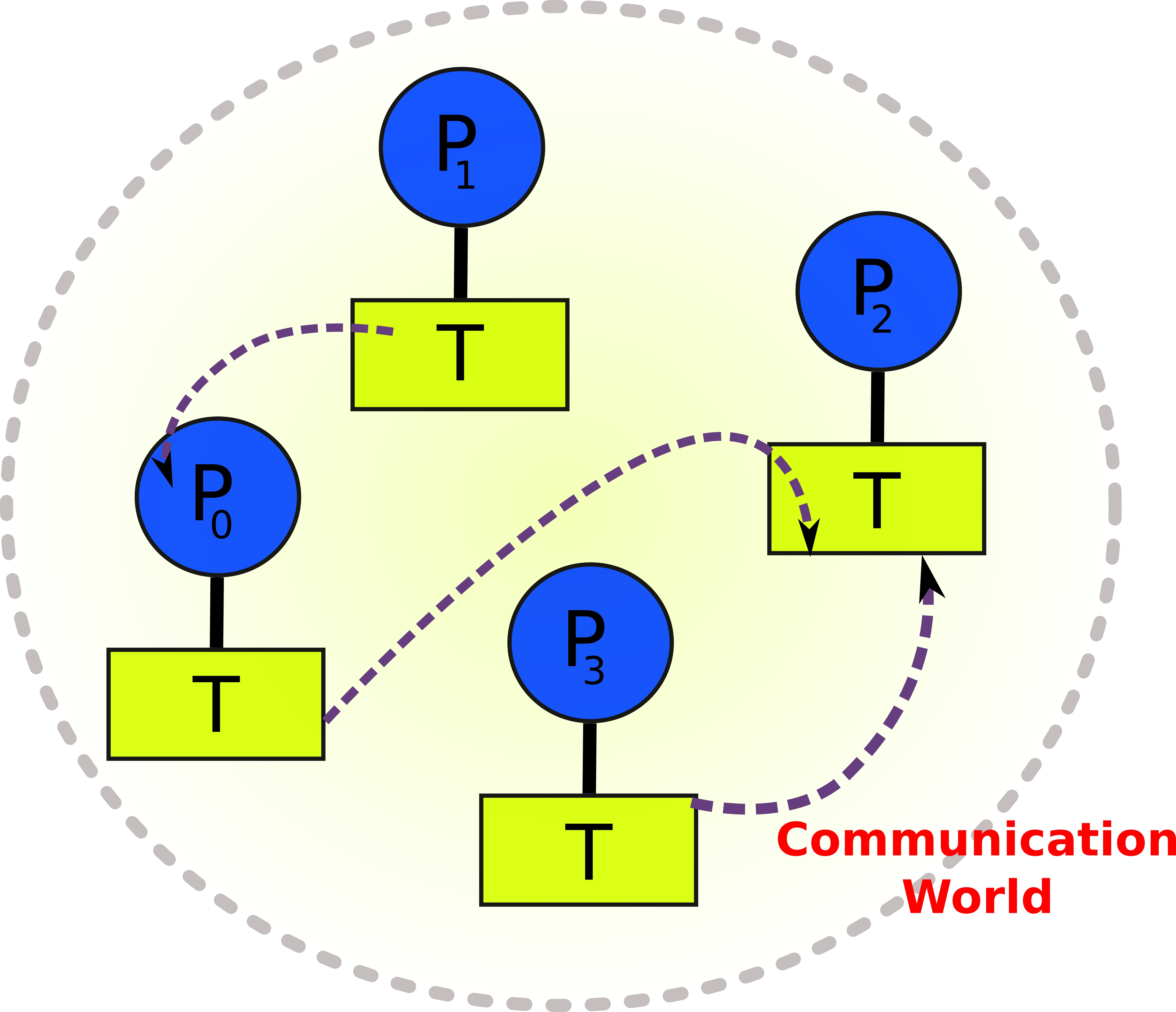
MPI characterized
- Processes that can send each other messages.
- There are many functions that facilitate this (mpi_send, mpi_recv etc).
- Different languages have wrappers around MPI for ease of use.
- For example, Rmpi for R.
GPU
- Good at many simple arithmetic operations.
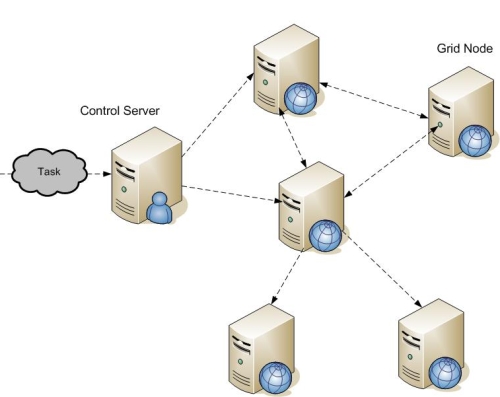
Grid computing
Comparisons
- Speed:
- Multithreading \\(\sim\\) GPU > MPI* > Grid
- Implementation in R (">" = faster)
- Multithreading > MPI > \\(\rr{GPU}=\rr{Grid}= \infty \\)
Multithreading is easy with R package multicore.
*MPI can be fast when using CPU cores are workers.
Main aspects
- Multithreading is fast but limited to the number of threads per processor.
- MPI is limited by the internode communication overhead, but clusters can (and are) constructed with low inter-node communication cost.
- GPUs are hard to program (CUDA), but are very fast at repeated simple calculations.
- Grids have very slow communication speeds, but can have massive numbers of computers.
Where Hadoop comes in
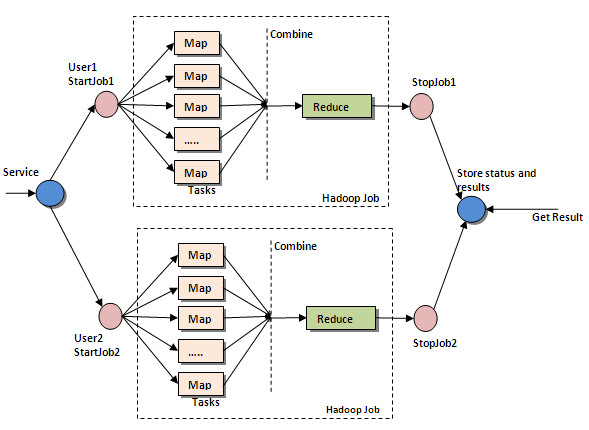
Other Hadoop-like things
- Father Big Table
- Hive
- Pig
- HBASE
- Many others
- Does it matter?
Services for distributed computing
- Infrastructure costs are low
- Amazon AWS (rocks)
- Multitude of vendors
Why we focus on MPI
- Rapidly becoming common
- Accessible implementations (R, Python, C++11)
- Clusters are becoming faster
- It is intuitive and less restrictive
R libraries for parallel computing
- multicore (very useful for emb. parallelization)
- snow, snowfall
- Rmpi
Embarrassingly parallel computing
- Run several independent jobs in parallel, collect the results
- Parallel sapply (mpi.applyLB)
- What we've been doing on Odyssey
Rmpi code snippets
#mpi.applyLB
x=1:7
mpi.applyLB(x, rnorm, mean = 2, sd = 4)
#get the same simulation
mpi.remote.exec(set.seed(111))
mpi.applyLB(x, rnorm, mean = 2, sd = 4)
#mpi.parApply
x=1:24
dim(x)=c(2, 3, 4)
mpi.parApply(x, MARGIN=c(1, 2), fun = mean, job.num = 5)Non-embarrassingly parallel (NEP) computing
- This is when the worker nodes communicate with each other in the process of executing the jobs.
- Such scheme is generally more robust as can be designed not to depend heavily on master node.
- It's also lower-level and trickier to implement and debug.
NEP computing is tricky
- Why is it so? Student discussion.
Code snippets
mpi.isend(x, type, dest, tag, comm = 1, request=0)
mpi.irecv(x, type, source, tag, comm = 1, request = 0)These are non-blocking calls.
Basic examples:
#on a slave
mpi.send(1:10, 1, 0, 0)
#on master
x <- integer(10)
mpi.irecv(x, 1, 1, 0)
x
mpi.wait()
xParallel statistical computing
- A generic question "how can I speed things up?"
- Starts with "going back to the blackboard"
- Not just MPI
Parallel likelihood calculation within MCMC
- Document authorship example
$$\begin{align}l(\alpha, \mu, \pi & \given y) \propto \sum_{w=1}^W\left[y_{dw}\rr{log}\left(\sum_k\mu_{kw}\pi_{dk}\right)\right. \\ & \left. -\sum_k\mu_{kw}\pi_{dk}\right] + \sum_{k=1}^K (\alpha_k - 1)\rr{log}\pi_{dk}\end{align}$$
Examples of parallelizable algorithms
- Parallel Tempering
- Equi-energy sampler
Parallel Tempering

Other ways to speed things up
- Faster code/languages
Announcements
- T-shirt competition winner!
- April 4 second final project submission deadline.
Resources
- Slides nesterko.com/lectures/stat221-2012/lecture17
- Class website theory.info/harvardstat221
- Class Piazza piazza.com/class#spring2013/stat221
- Class Twitter twitter.com/harvardstat221
Final slide
- Next lecture: Parallel Tempering - nuts and bolts.
