Decision Theory and Statistical Inference
Stat 221, Lecture 16
Roadmap
- Decision Making based on Inference
- Relevance to multimodality
- Case study - marketing campaigns optimization
Where we are
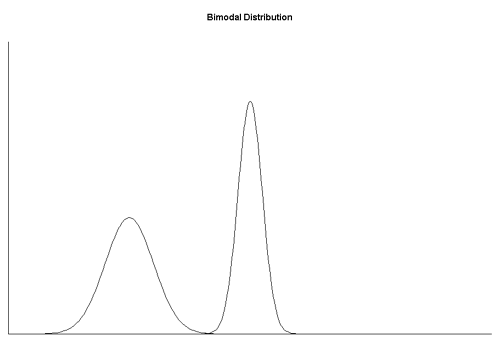
In the presence of multimodality, maximum likelihood breaks down
- We use the full likelihood/posterior to get information about the parameters that describe the system.
- But how exactly do we use it to make decisions where the parameter values are inputs?
- One step beyond inference.
Example: IT materials for schools
- The data is binary - students getting into college or not.
- Interested in a parameter - association of time spent on IT materials and getting into college.
- Fit a logistic regression-like model to check that.
Slope posterior distribution
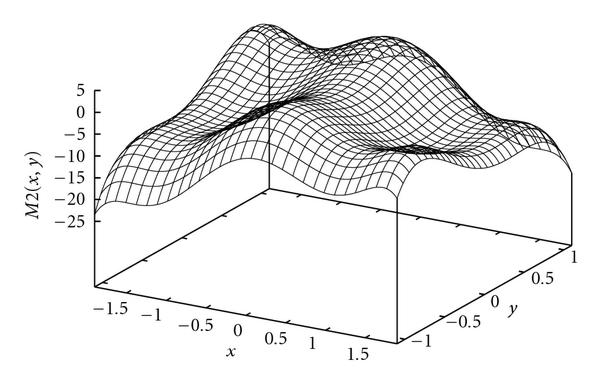
Could be more complicated
Questions
- Are there two groups of people in the class?
- Is this an artifact of the model?
- So how many IT materials should we order?
Ex.: running man HMM
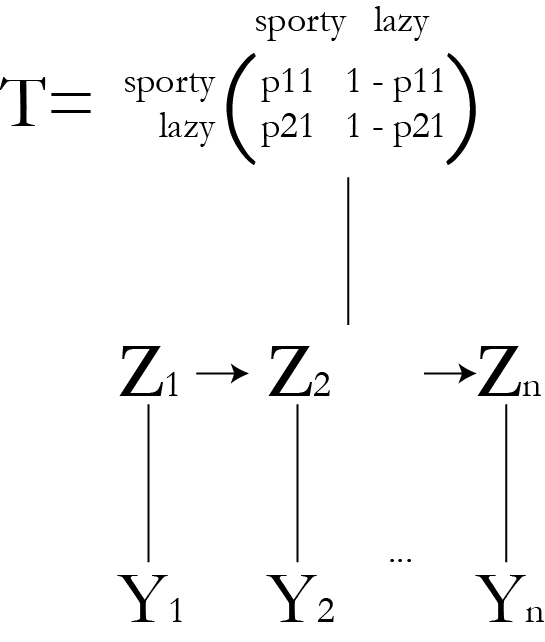
Non-identifiability even in this simple model.
Introduction to Decision Theory
- There is "cost" to each decision.
- Some would call it a game "statistician against nature".
- The cost is postulated via a loss function.
- The cost depends on the underlying true value of the parameter.
Classic cost functions
Squared error $$ C(\theta, d) = (d - \theta)^2 $$
Absolute error $$C(\theta, d) = | d - \theta | $$
Constant error $$ C(\theta, d) = A \cdot I_{|d - \theta| > \epsilon} $$
In the IT materials example, what cost function would we choose?
- What other ways could we employ to plan the next IT materials order?
Definitions
Let \\( \delta (y) \\) stand for a decision we make based on data.
Define risk function \\( R_\delta(\theta) \\)
$$R_\delta(\theta) = \rr{E}_\theta \left[ C\left(\theta , \delta\left(y \right) \right)\right]$$
Admissibility
A decision rule \\( \delta \\) is admissible if there exists no another decision rule \\( \tilde{\delta} \\) where \\( R_{\tilde{\delta}}(\theta) \leq R_{\delta}(\theta) \\) for all \\( \theta \in \Theta \\), with the inequality strict for at least one \\( \theta \\).
Example
- Interval parameter space \\( \Theta = [0, 1] \\).
- Assume Mean Squared Error loss.
- Can we find decision rule that has a minimal MSE uniformly over \\( \Theta \\)?
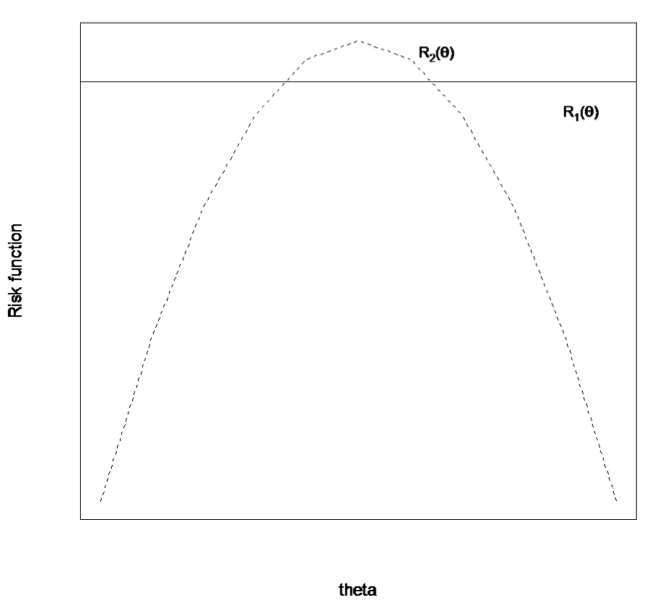
Minimaxity
The decision rule \\( \delta \\) is minimax if for any other decision rule \\( \tilde{\delta} \\), the risk function for \\( \delta \\) satisfies
$$\mathop{\rr{sup}}_{\theta \in \Theta} \{ R_\delta(\theta)\} \leq \mathop{\rr{sup}}_{\theta \in \Theta} \{ R_{\tilde{\delta}}(\theta)\}$$
Which one is minimax?
Bayesian Decision Analysis
Bayes risk is
$$\rr{E}_\pi \left[ R_\delta (\theta)\right] = \int_\Theta R_\delta (\theta) \pi(\theta) d\theta$$
This is a double expectation, averaged both through data \\( y \\) and parameter \\( \theta \\).
Rearrange
$$\begin{align} \rr{E}_\pi \{ R_\delta (\theta)\} & = \int \int C(\theta, \delta(y)) f(y \given \theta) dy \pi(\theta) d\theta \\ & = \int \int C(\theta, \delta(y)) p(\theta \given y) f(y) d \theta dy \\ & = \int f(y) \int C(\theta, \delta(y)) p(\theta \given y) d \theta dy\end{align}$$
Minimizing Bayes risk is equivalent to minimizing the posterior expectation of the loss function.
Convenience of Bayes risk
- It defines a single number.
- So, it's easy to look for the best decision rule - just look for the one with the lowest Bayes risk.
Theorem
- Any Bayes rule corresponding to a proper nondogmatic prior \\( \pi (\theta) \\) is admissible.
This means Bayesian procedures are admissible in the frequentist sense.
Example
Minimize the Bayes Risk with respect to squared error loss.
$$\rr{argmin}_\delta \left\{ \int \left( \theta - \delta(y)\right)^2 p(\theta \given y) d\theta \right\}$$
Let's find the corresponding decision rule.
Calculations
$$\begin{align}\int \left( \theta - \delta(y)\right)^2 & p(\theta \given y) d\theta \\ = & \rr{Var} \left[ \theta - \delta(y) \given y \right] + \\ & \left( \rr{E} \left[ \theta - \delta(y) \given y \right]\right)^2 \\ = & \rr{Var} \left[ \theta \given y \right] + \left( \rr{E} \left[ \theta \given y \right] - \delta(y)\right)^2\end{align}$$
From here it's evident that the posterior mean minimizes mean squared loss.
However, is the posterior mean really what we want when the posterior surface is irregular?
Student discussion.
Inferential decisions
- When doing point estimation
- Usually, this means we are minimizing mean squared error.
- This allows for the handy bias-variance tradeoff intuition.
- When doing full posterior inference
- We get full draws from the posterior surface.
- Often, we collapse that information down into posterior mean and variance.
- Is this practical? Is there middle ground?
Example: bimodal posterior
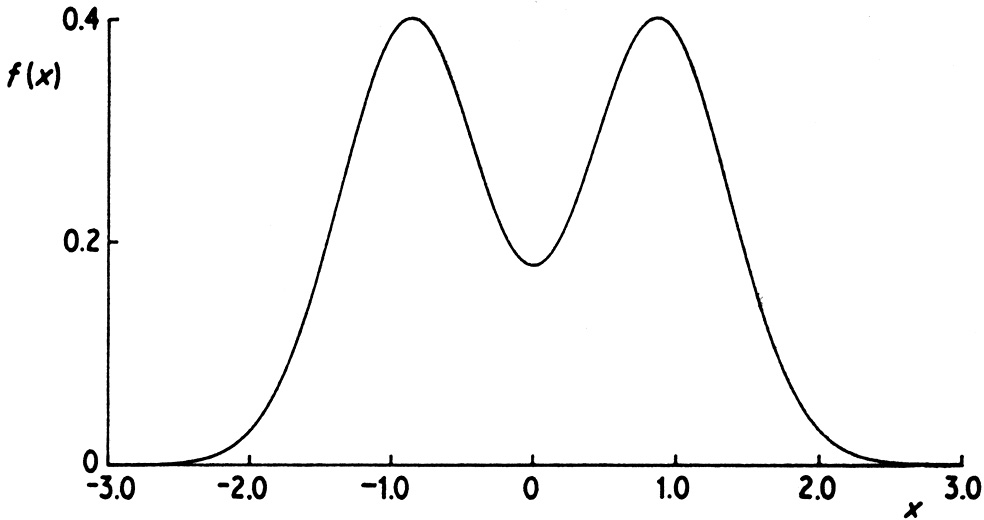
One option: custom cost functions
- Follow decision theory paradigm and define a loss function that we care about.
- Use the full information provided by the posterior surface to arrive at an optimal decision.
- But let's not get carried away! There are serious risks to blindly doing this.
Case study: marketing optimization
- A large CPG manufacturer wants to link its marketing campaigns to revenue.
- Further, they want to make the next year's marketing campaigns better.
- Possible solutions:
- Randomized experiments + response surface methods
- RCM
- Decision theory?
Model statements
- Revenue \\( R \\) as a function of promotion campaigns:
$$R \given \theta, X \sim f(\theta, X)$$
- For example, regression-like model $$\rr{log} R \given \beta, X \sim X\beta + \epsilon$$
- This allows to obtain the posterior $$p(\theta \given R, X)$$
- The posterior is the information about model parameters as provided by the data subject to the model formulation.
Futher, optimize marketing allocation for next year
Define a suitable cost function and optimize its posterior expectation with respect to \\( \delta(X) \\)
$$ \int C(\theta, \delta(X)) p(\theta \given R, X) d \theta$$
What cost function should we define?
Cost function
There are several ways (simple regression example):
- Link to mean revenue $$C(\theta, \delta(X)) = -\rr{exp} \left\{ \delta(X)\beta\right\}$$
- Link to resource reallocation costs
$$C(\theta, \delta(X)) = -\rr{exp} \left\{ \delta(X)\beta\right\} + L(\delta(X))$$
- How to we define \\( L \\)?
- Incorporate nonlinearity
Optimization
Once we've decided on our cost, need to find \\( \delta(X) \\)
- Complex optimization
- The CPG manufacturer has 100 brands with up to 300 product items each, there are 30 markets, 52 weeks, 7 promotion campaigns
- In total, this is $$327,600,000 \approx 320\rr{M} \rr{ dimensions}$$
- Add to this that this needs to be done at each point in the parameter space.
Issues
- Computational issues - how do we do this?
- Validity concerns
- What are the alternative ways to go?
Further resources
- Causal Inference, Don Rubin
- Response Surface Methodology, Myers et al
- Parallel computing
Announcements
- T-shirt comps!
- April 4 second final project checkpoint
Resources
- Slides nesterko.com/lectures/stat221-2012/lecture16
- Class website theory.info/harvardstat221
- Class Piazza piazza.com/class#spring2013/stat221
- Class Twitter twitter.com/harvardstat221
Final slide
- Next lecture: Parallel statistical computing.
