Hamiltonian Monte Carlo
Stat 221, Lecture 15
Where we are
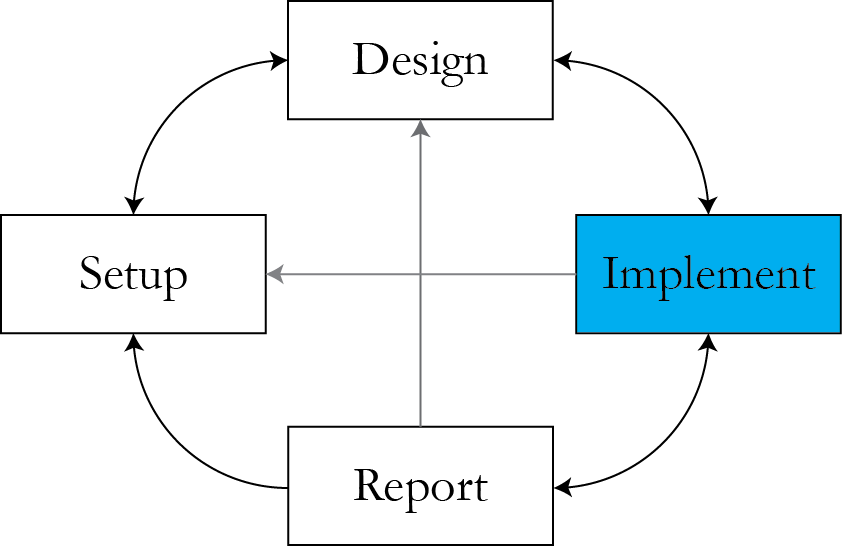
Reference for the lecture
- Radfor Neal's review of HMC.
HMC: notation
- We want to simulate \\( \theta \equiv q \\) from \\( p(\theta \given Y) = \pi(\theta) L(\theta \given Y)\\).
- Augment \\( \theta \\) space - each element of \\( q \\) gets a corresponding "brother" \\( p \\).
- Potential energy function (linked to the posterior) $$U(q) = -\rr{log} \left( p (q \given Y)\right)$$
- Kinetic energy function (negative log-density of momentum variables) \\( K(p) \\).
Main intuition
In the Hamiltonian system, the sum of kinetic enery \\( P \\) and potential energy \\( U \\) is constant.
(we work on the log scale)
HMC: how it works

HMC algorithm
Two steps:
- Draw new momentum variables \\( p^* \\) from the distribution (usually Gauggian) defined by the kinetic energy function.
- Propose a new state \\( q^* \\) for position variables \\( q \\) by simulating Hamiltonian dynamics given the momentum \\( p \\) and the current value of \\(q\\). Accept with probability
$$\rr{min}\left[ 1, \rr{exp}\left( -U(q^*) + U(q) - K(p^*) + K(p) \right)\right]$$
The Hamiltonian
$$\begin{align} {dq_i \over dt} & = {\partial H \over \partial p_i} \\ {dp_i \over dt} & = -{\partial H \over \partial q_i}\end{align}$$
Most commonly used form of \\( H \\): $$ H(q, p) = U(q) + K(p) $$
Kinetic and potential energies
Usual choice for the kinetic energy $$K(p) = p^T M^{-1} p / 2$$
What distribution does this correspond to?
Potential energy $$U(q) = -\rr{log} \left( p (q \given Y)\right)$$
Hamiltonian narrowed down
Given the defined \\( H \\) and \\( K \\), the Hamiltonian equations become the following:
$$\begin{align} {dq_i \over dt} & = \left[ M^{-1} p\right]_i \\ {dp_i \over dt} & = -{\partial U \over \partial q_i}\end{align}$$
A 1D example
$$H(q, p) = U(q) + K(p)$$
\\( U(q) = {q^2 \over 2}, K(p) = {p^2 \over 2} \\) - what are the pdfs?
Hamiltonian: $${dq \over dt} = p, \rr{ } {dp \over dt} = -q$$
Solution, for some \\(r \\) and \\(a \\):
$$q(t) = r\rr{cos}(a + t), \rr{ } p(t) = -r \rr{sin} (a+t)$$
Interpretation
- The Hamiltonian trajectory travels the level set of the joint momentum-position density.
Main properties of Hamiltonian dynamics
- Reversibility.
- Conservation of the Hamiltonian.
- Volume preservation.
Reversibility
- Mapping \\( T_s \\) from state at time \\( t \\) to state at time \\( t + s \\) is one-to-one, and has an inverse ( \\( T_{-s} \\) ).
- With the considered form of the Hamiltonian and \\( K(p) = K(-p) \\), \\( T_{-s} \\) can be obtained by negating \\( p \\), applying \\( T_s \\), and negating p again.
- In the 1D example, \\( T_{-s} \\) is the counter-clockwise rotation.
- This implies that MCMC using HMC dynamics leaves desired distribution invariant.
Conservation of the Hamiltonian
$$\begin{align}{dH \over dt} &= \sum_{i=1}^d \left[ {d q_i \over dt} {\partial H \over \partial q_i} + {d p_i \over dt} {\partial H \over \partial p_i}\right] \\ & = \sum_{i=1}^d \left[ {\partial H \over \partial p_i} {\partial H \over \partial q_i} - {\partial H \over \partial q_i} {\partial H \over \partial p_i} \right] = 0\end{align}$$
- The trajectory travels the level set of the joint \\( qp\\) distribution.
- This means probability 1 of accepting a move given the Hamiltonian is simulated exactly.
Volume preservation
Vector field zero divergence:
$$\begin{align}\sum_{i=1}^d & \left[ {\partial \over \partial q_i} {d q_i \over dt} + { \partial \over \partial p_i} {d p_i \over dt}\right] = \\ & \sum_{i=1}^d \left[ {\partial \over \partial q_i} {\partial H \over \partial p_i} + { \partial \over \partial p_i} {\partial H \over \partial q_i}\right] = 0\end{align}$$
Don't need to use the Jacobian in the acceptance probability.
The leapfrog method
$$\begin{align}p_i(t + \epsilon / 2) & = p_i(t) - (\epsilon / 2) {\partial U \over \partial q_i}q_i(t) \\ q_i(t + \epsilon) & = q_i(t) + \epsilon {p_i(t + \epsilon / 2) \over m_i} \\ p_i(t + \epsilon) &= p_i(t + \epsilon / 2) - {\epsilon \over 2} \cdot { \partial U \over \partial q_i} q_i(t + \epsilon)\end{align}$$
Here \\( K(p) = \sum_{i=1}^d { p_i^2 \over 2m_i } \\).
Example: homework
$$\begin{align} & l(B, \vec{Z}_i \given \{C_{ijk}\} ) = \rr{const} + \\ & \sum_{i=1}^I \left( \sum_{j \in J_i} \sum_{k \in K_{ij}} \left[ \vec{x}_{jk}' B - \rr{log} \sum_{l = 1}^{L_j} e^{ \vec{x}_{jl}' B} \right] \right) \cdot \vec{Z}_i \end{align}$$
\\( U = - \rr{log} l \\), \\( q = B \\).
How to implement
- Sample code in Neal's review (p. 14).
- Generic sample code for a vector case - ask TF's.
The leapfrog method
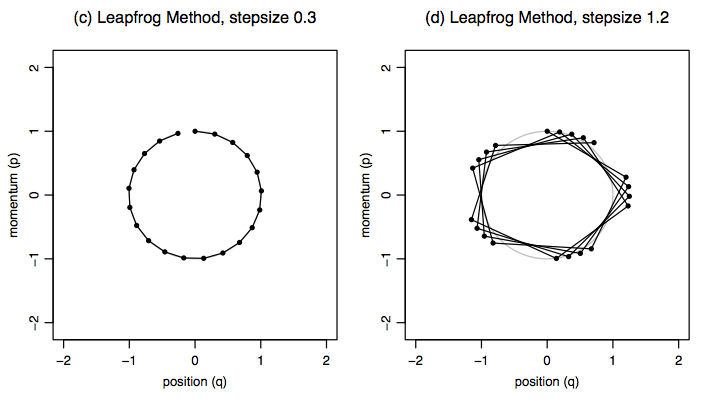
Detailed balance in HMC
$$P(A_i) T(B_j \given A_i) = P(B_j) T(A_i \given B_j)$$
\\( B_k\\) be the image of \\( A_k\\) after \\( L \\) leapfrog steps and negating the momentum.
\\( P \\) is the probability under the canonical distribution, \\( T(X \given Y ) \\) is the conditional probability of proposing and then accepting a move to region \\( X \\) if the current state is in region \\( Y \\).
Example: bivariate Normal
$$H(q, p) = q^T \Sigma^{-1} q / 2 + p^T p / 2$$
with $$\Sigma = \left(\begin{array} n1 & 0.98 \\ 0.98 & 1\end{array} \right)$$
What position distribution does this correspond to?
Trajectories
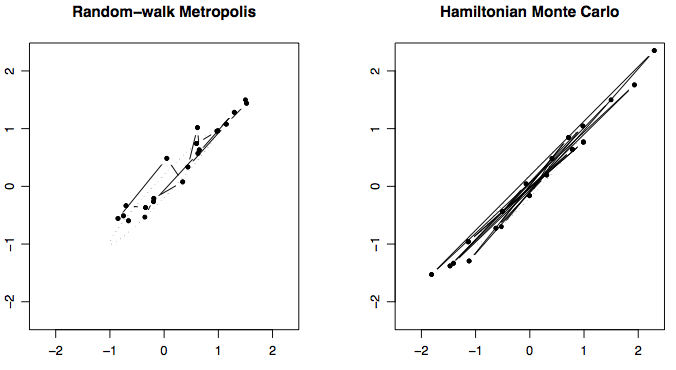
Trace plots
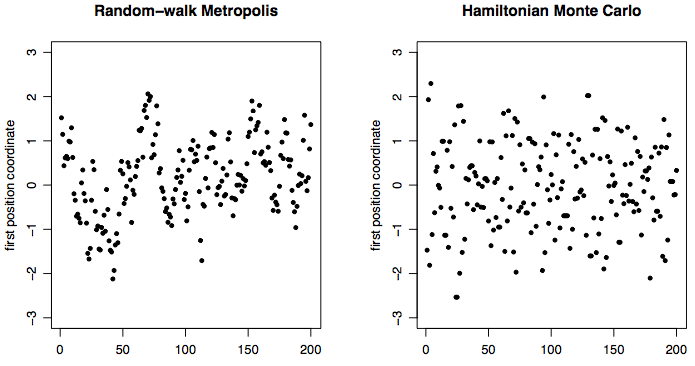
100D Normal
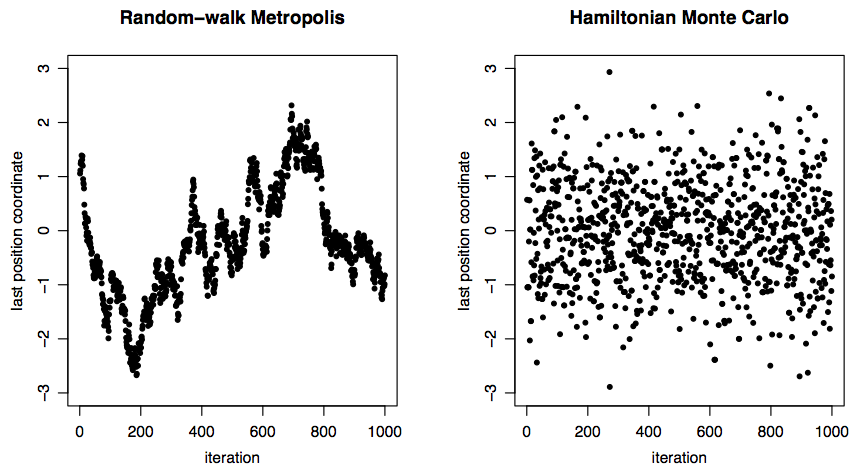
Further improvements to HMC
- Use target Hessian to set the Mass matrix.
- No U-turn sampler.
- Other.
HMC and the Hessian
- Compute the Hessian at a local mode of the posterior.
- Effectively, this corresponds to "uncorrelating" the parameters.
Computational aspects of HMC
- Number of steps and step size: \\( l \\) and \\( \epsilon \\).
- Need to compute the posterior and gradient many times.
- For good implementations of HMC, need to compute the Mass matrix.
Mass/trajectory approximation tradeoff
- If the mass matrix is bad, need better leapfrog approximation.
- What is better - good mass or crude approximation of Hamiltonian dynamics?
Extensions of HMC
- Bounded parameters
- Discrete parameters
Limitations
- Still prone to local modes.
- But if the modes are even somewhat connected, it's much better than MH!
Augmentation strategies
- Hacker level
- Parameter expansion - adding fixed parameters (PX-EM, vEM)
- Data augmentation - adding random quantities (HMC, parallel/simulated tempering)
- It's all data augmentation in the Bayesian paradigm
Announcements
- T-shirt comps!
- April 4 - final project second checkpoint deadline.
- Set up time over email to check that final projects are on track.
Resources
- Slides nesterko.com/lectures/stat221-2012/lecture15
- Class website theory.info/harvardstat221
- Class Piazza piazza.com/class#spring2013/stat221
- Class Twitter twitter.com/harvardstat221
Final slide
- Next lecture: Desicion theory and estimation.
