Missing data and MCMC, HMC
Stat 221, Lecture 14
Where we are
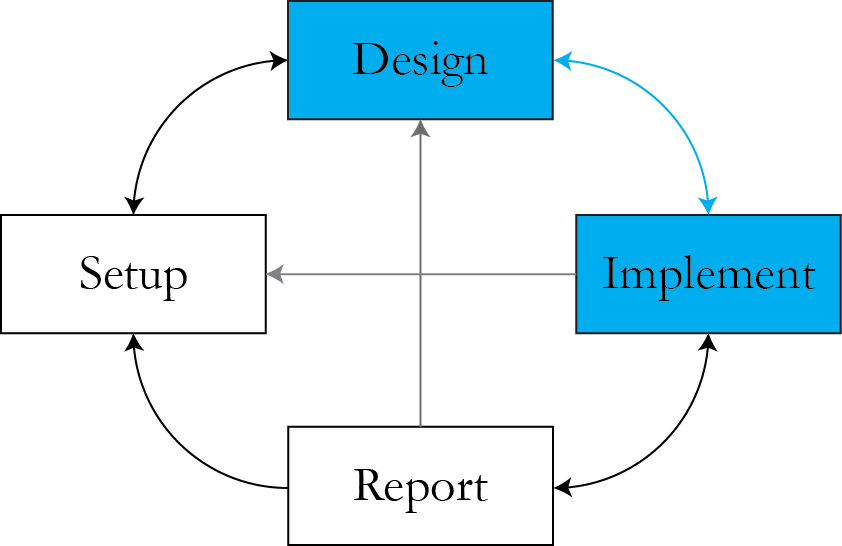
- Implementation immediately feeds back into design!
MCMC and missing data
- EM integrates over the missing data. $$\begin{align}Q\left( \theta | \theta^{(t)} \right) = \int l(\theta | y) f( Y_{\rr{mis}}| Y_{\rr{obs}}, & \theta = \theta^{(t)}) \\ & dY_{\rr{mis}} \end{align}$$
- MCMC can help do the same.
- Draw missing data as if they were parameters.
Maximizing over missing data?
- Taking something the model says is random and treating it as unknown constant.
- Can lead to problems if the number of parameters grows with the number of data points (Neyman-Scott problem).
- MLE efficiency conditions break down.
Gelman radon detectors
- Radon level of house \\( i \\) in the neighborhood is \\( \mu_i \sim \rr{N}\left( \mu_0, \sigma_0^2\right)\\).
- \\( \mu_0 \\) is the mean neighbourhood radon level, \\( \sigma_0 \\) is the spread of individual house radon measurements around the neighborhood mean.
- Conditional on the true house radon level, the detector measures it with error: $$y_i \given \mu_i \sim \rr{N} \left( \mu_i, \sigma^2\right)$$
Neyman-Scott problem
- There is one \\( \mu_i \\) for each \\( y_i \\).
- This leads to inconsistent estimate of \\( \sigma_0^2 \\).
EM as a half-Bayesian method
- What part of EM looks Bayesian?
mcEM
- Change the E step
- Replace \\( E (Y_{\rr{mis}} \given Y_{\rr{obs}}, \theta) \\) by its estimate
- Obtain the estimate by simulating from the distribution $$ f(Y_{\rr{mis}} \given Y_{\rr{obs}}, \theta) $$
- What are the possible caveats?
When to apply mcEM
- Quick and dirty approximate method.
- Hard to explicitly find the expected value in the E step.
Example: document authorship
- Document authorship \\( \pi_d \sim \rr{Dirichlet}_K(\vec{\alpha},1) \\).
- Data \\( y_{dw} \given \pi_d \sim \rr{Poisson}(\sum_k\mu_{kw}\pi_{dk})\\).
- Author \\( k\\), document \\( d \\), word \\( w \\).
- \\( \pi_{dk} \\) represents the amount of contribution of author \\( k \\) do document \\(d\\).
Likelihood
For document \\( d \\):
$$\begin{align}L(\alpha, \mu \given y, \pi) \propto & \prod_{w=1}^W\left[\left(\sum_k\mu_{kw}\pi_{dk}\right)^{y_{dw}} \right. \\ & \left.\cdot e^{-\left(\sum_k\mu_{kw}\pi_{dk}\right)}\right] \cdot \prod_{k=1}^K \pi_{dk}^{\alpha_k - 1}\end{align}$$
The expectation of the \\( Q \\) function is hard to get in closed form.
Caveats of mcEM
- Estimation of the expected values associated with the latent variables.
- Especially challenging for high-dimensional distributions, requires many MC iterations in the E step.
Full MCMC and EM connection
- Point estimation versus full posterior inference.
- Full MCMC erases the difference between a parameter and a latent variable.
- MCMC "contains" point estimation, EM can recreate the results of MCMC only under Normality (practically, never).
Non-normality
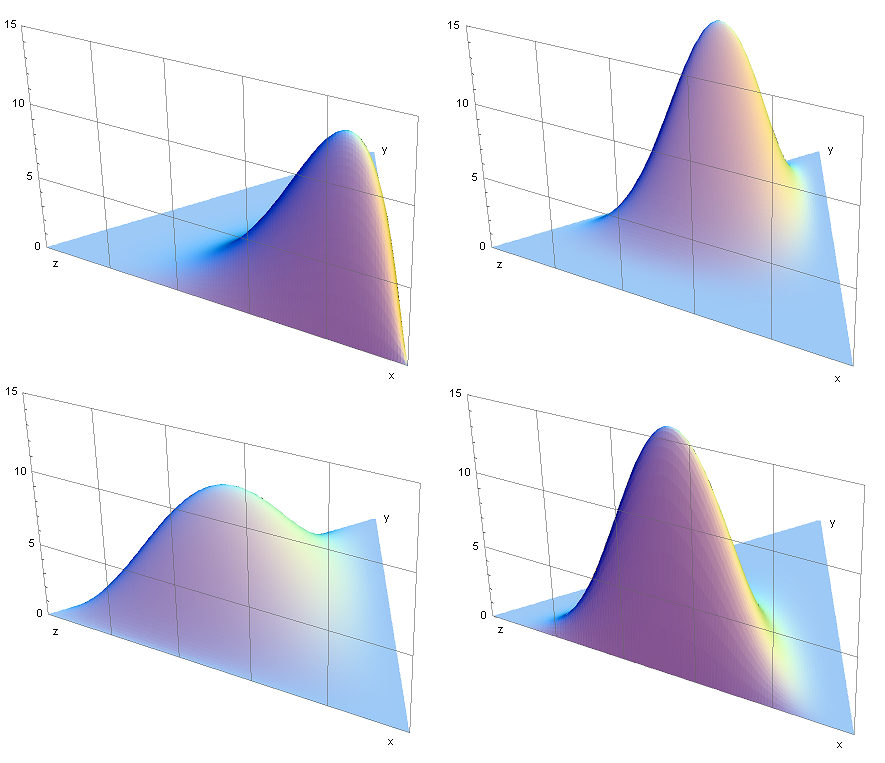
Discrete vs continuous rvs
Discrete rvs are special:
- Absence of the Jacobian when changing variables.
- Hard to construct symmetric jumping rules for MCMC in the discrete case.
- Discrete rvs are hard to deal with.
Example: HMMs
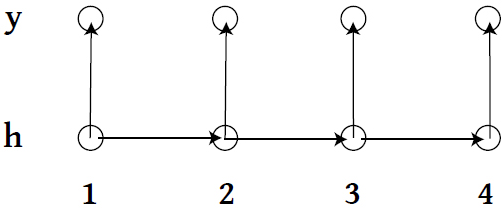
Drawing \\( h \\) is hard.
- Baum-Welch and full Bayes don't work well.
Posterior for HMMs
$$\begin{align}p(\theta, H \given Y ) \propto & f_{\theta}(y_1 \given h_1)g_\theta(h_1) \cdot \\ & \prod_{i=2}^n f_{\theta}(y_i \given h_i)g_\theta(h_i \given h_{i-1})\end{align}$$
- Even for a 2-state HMM, if a sample size is non-trivial (i.e. has \\( n > 10 \\)), it becomes hard to find high-probability \\( H \\) chains via MCMC (\\( 2^n \\) possible chains).
Hamiltonian Monte Carlo
- MCMC to sample from distributions of continuous rvs.
- Uses data augmentation strategy (hacker level!).
- Leverages physics to get draws far away from the initial values.
Example: Cauchy model
$$y_i \given \theta \mathop{\sim}^{\rr{ind}} { 1 \over (y_i - \theta)^2 + 1 }$$
Observe data \\( y_1 = 4, \rr{ } y_2 = -4 \\). Posterior:
$$p(\theta \given Y) \propto { 1 \over (4 - \theta)^2 + 1 } \cdot { 1 \over (4 + \theta)^2 + 1 }$$
- Bimodal distribution.
HMC: how it works on Cauchy model

Summary of HMC
- Simulates Hamiltonian dynamics.
- Moves around the space faster.
- "Strictly better" than classic Metropolis for continuous rvs (converges faster, smaller autocorrelation).
- Like classic Metropolis, gets trapped in local modes.
Questions inspired by HMC
- Is there an equivalent for discrete rvs?
- How do we deal with separated local modes?
Announcements
- T-shirt comp!
- Use Piazza, share ideas about homework.
- Pset4 due next Wednesday.
- Final project: method design meetings, end-of-semester presentation.
Resources
- Slides nesterko.com/lectures/stat221-2012/lecture14
- Class website theory.info/harvardstat221
- Class Piazza piazza.com/class#spring2013/stat221
- Class Twitter twitter.com/harvardstat221
Final slide
- Next lecture: HMC nuts and bolts
