EM for HMMs, properties of EM

Stat 221, Lecture 11

@snesterko

Emphasis of this lecture

EM for HMMs - forward-backward algorithm.
Thinking about R-friendly ways to perform computation.
Understanding the benefits and limitations of EM in non-trivial settings.

Roadmap

Derive EM for HMMs.
Make a break to critique a visualization on EM (homework).
Keep deriving EM for HMMs and thinking about the relationship with computing and inference:
- How to do HMM EM computation faster in R?
- Does the HMM EM ever converge?

EM for HMMs

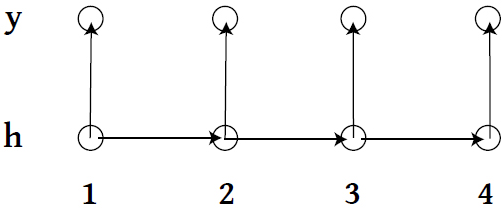
\$\{h_1, h_2, \ldots \} \$ live on discrete space, follow a Markov Process with a transition matrix \$ A \$.
At time \$ t\$, state \$ h_t \$ emits observation \$ y_t \$ according to some specified model.

A different view

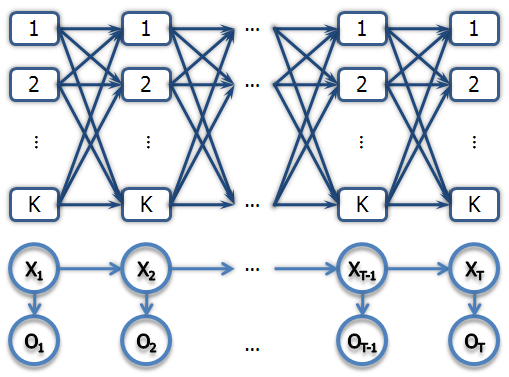
Notation change

To be consistent with Bishop pp. 610-625.
Observed data \$ X \$.
Hidden states \$ Z \$.
Hidden states transition matrix \$ A_{k \times k} \$.

Complete-data likelihood

$$\begin{align}p(X, Z \given \theta) \propto & p(x_1 \given z_1, \phi)p(z_1 \given \pi) \cdot \\ & \prod_{n=2}^N p(z_n \given z_{n-1}, A)p(x_n \given z_n, \phi)\end{align}$$

Running man HMM

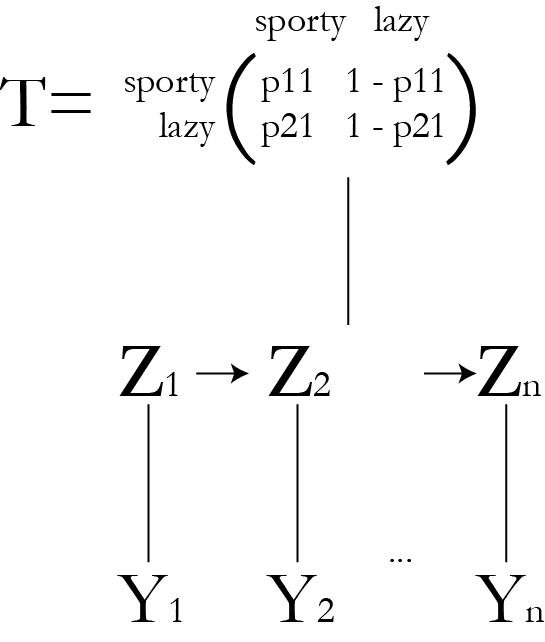
Complete data likelihood

Let \$ N = 3 \$.

$$\begin{align} L(\theta \given X, Z ) \propto & \left(\rr{Bern}(x_1|p_l)\right)^{z_1}\left(\rr{Bern}(x_1|p_s)\right)^{1-z_1} \\ \prod_{i=2}^3 & \left(\rr{Bern}(x_i|p_l)\right)^{z_i}\left(\rr{Bern}(x_i|p_s)\right)^{1-z_i} \\ & \cdot T(z_i \given z_{i-1})\end{align}$$

Observed-data likelihood

$$p(X \given \theta) \propto \sum_{Z} p(X, Z \given \theta)$$

Need to sum over \$ K^N \$ terms.
Impractical to do this directly.

Observed data likelihood

\$ Z = \{ (0, 0, 0), (0, 0, 1), (0, 1, 0), \ldots, (1, 1, 1)\} \$ - \$ 2^3 = 8\$ terms

$$\begin{align} L \propto & \sum_{z \in Z} \left[\left(\rr{Bern}(x_1|p_l)\right)^{z_1}\left(\rr{Bern}(x_1|p_s)\right)^{1-z_1} \right.\\ \prod_{i=2}^3 & \left(\rr{Bern}(x_i|p_l)\right)^{z_i}\left(\rr{Bern}(x_i|p_s)\right)^{1-z_i} \\ & \left.\cdot T(z_i \given z_{i-1}) \right]\end{align}$$

Define

\$ \gamma (z_n) = p (z_n \given X, \theta^{(old)}) \$
\$ \xi (z_{n-1}, z_n) = p (z_{n-1}, z_n \given X, \theta^{(old)}) \$
Also let
- \$ \gamma( z_{nk}) = P( z_{nk} = 1 \given X, \theta^{(old)}) \$ - conditional probability that \$ Z_n \$ is in state \$ k \$.
- \$ \xi( z_{n-1,j}, z_{nk}) = \$ \$P( z_{n-1,j} = 1, z_{nk} = 1 \given X, \theta^{(old)}) \$ - conditional probability that \$ Z_{n-1} \$ is in state \$ j \$ and \$ Z_n \$ is in state \$ k \$.

\$ \gamma \$ and \$ \xi \$ in the example

\$ \gamma (z_{n1}) = P(\rr{lazy on day }n \given X, \theta^{(old)}) \$
\$ \xi (z_{n-1, 1}, z_{n2}) = P(\rr{lazy on day }n-1, \$ \$ \rr{ sporty on day }n \given X, \theta^{(old)}) \$
\$ X \$ - observed running data.
\$ \theta^{(old)} \$ - past iteration of HMM transition parameters of \$ A \$ and emission parameters.

\$ Q \$ function

$$\begin{align}Q(\theta, \theta^{(old)}) = & \sum_{k=1}^K\gamma(z_{1k})\rr{log} \pi_k + \\ & \sum_{n=2}^N \sum_{j=1}^K \sum_{k=1}^K \xi(z_{n-1, j}, z_{nk}) \rr{log} A_{jk} \\ & + \sum_{n=1}^N \sum_{k=1}^K \gamma(z_{nk}) \rr{log} p( x_n \given \phi_k) \end{align}$$

Example \$ Q \$ function

$$\begin{align}Q(\theta, \theta^{(old)}) = & \sum_{k=1}^2\gamma(z_{1k})\rr{log} 0.5 + \\ & \sum_{n=2}^3 \sum_{j=1}^2 \sum_{k=1}^2 \xi(z_{n-1, j}, z_{nk}) \rr{log} A_{jk} + \\ & \sum_{n=1}^3 \sum_{k=1}^2 \gamma(z_{nk}) \rr{log} \rr{Bern}(x_i|(p_l /p_s)) \end{align}$$

M step

Constraint: \$ \pi \$ and rows of \$ A \$ need to sum to 1.

$$ \pi_k = \frac{\gamma(z_{1k})}{\sum_{j=1}^K \gamma(z_{1j})} $$

$$ A_{jk} = \frac{\sum_{n=2}^N \xi(z_{n-1,j}, z_{nk})}{\sum_{l=1}^K \sum_{n=2}^N \xi(z_{n-1, j}, z_{nl})}$$

The weighting is common in EM algorithms. Likelihood weights.

Example transitions M step

Prior is flat, so nothing for \$ \pi \$.
Same for the transition probabilities: $$ A_{jk} = \frac{\sum_{n=2}^N \xi(z_{n-1,j}, z_{nk})}{\sum_{l=1}^K \sum_{n=2}^N \xi(z_{n-1, j}, z_{nl})}$$

M step for emission params

$$ \mu_k = \frac{\sum_{n=1}^N\gamma(z_{nk}) x_n}{\sum_{n=1}^N \gamma(z_{nk})} $$

$$ \Sigma_k = \frac{\sum_{n=1}^N\gamma(z_{nk}) (x_n - \mu_k)(x_n - \mu_k)^T}{\sum_{n=1}^N \gamma(z_{nk})} $$

This is for the Normal emission case.

Example emission M step

Sporty running probability:

$$ p_s = {\sum_{n=1}^3 \gamma(z_{n1}) x_n\over \sum_{n=1}^3 \gamma(z_{n1}) }$$

Lazy running probability:

$$ p_l = {\sum_{n=1}^3 \gamma(z_{n2}) x_n\over \sum_{n=1}^3 \gamma(z_{n2}) }$$

Breather: EM and KL divergence

+ visualization critique

EM algorithm for linear regression.

Conditional independence properties

$$\begin{align} p(X \given z_n) = & p(x_1, \ldots, x_n \given z_n) \cdot \\ & p(x_{n+1}, \ldots, x_N \given z_n) \\ p(z_{N+1} \given z_N, X) = & p(z_{N+1} \given z_N) \end{align}$$

Others.

Note that

$$\gamma (z_n ) = p(z_n \given X) = { p(X \given z_n)p(z_n) \over p(X)}$$

All this is conditional on \$ \theta^{\rr{old}} \$, so \$ p(X) \$ is the likelihood.

Then

$$\gamma(z_n) = {p(x_1, \ldots, x_n, z_n) p(x_{n+1}, \ldots, x_N \given z_n) \over p(X)}$$

Definitions

\$ \alpha ( z_n ) \equiv p(x_1, \ldots, x_n, z_n) \$
\$ \beta (z_n) \equiv p(x_{n+1}, \ldots, x_N \given z_n)\$

Example \$ \alpha \$ and \$ \beta \$

\$ \alpha \$ is the probability of observing a given sequence of running behavior up to time \$ n \$ and a specific lazy/sporty state at time \$ n \$.
\$ \beta \$ is the probability of observing a future sequence of running behavior after time \$ n \$ given a specific lazy/sporty state at time \$ n \$.

Forward recursion

$$\begin{align}\alpha(z_n) = &p(x_n|z_n) \cdot \\ & \sum_{z_{n-1}} p(x_1, \ldots, x_{n-1}, z_{n-1}) p(z_n|z_{n-1})\end{align}$$

$$\alpha(z_n) = p(x_n \given z_n) \sum_{z_{n-1}} \alpha(z_{n-1}) p(z_n \given z_{n-1})$$

Initial condition: $$\alpha(z_1) = p(x_1, z_1) = \prod_{k=1}^K \left\{ \pi_k p(x_1 \given \phi_k)\right\}^{z_{1k}}$$

Backward recursion

$$\beta(z_n) = \sum_{z_{n+1}} \beta(z_{n+1}) p(x_{n+1} \given z_{n+1}) p(z_{n+1} \given z_n)$$

Take initial condition from

$$p(z_N \given X) = { p(X, z_N) \beta(z_N) \over p(X)}$$

So, set \$ \beta(z_N) = 1 \$ for all settings of \$ z_N \$.

R-friendly calculations

Remember, \$ \alpha \$ and \$ \beta \$ ech have \$ K \$ components.
How can we perform a step of say \$ \beta \$ recursion in an R-friendly way?

Example recursions

The algorithm is generic, only the emissions change from one implementation to the next.

\$ \beta(z_3) \$ initial condition is straightforward: a vector of 2 1's.
\$ \alpha(z_{11}) = 1/2\cdot p_s^{x_1} (1 - p_s)^{1-x_1}\$, \$ \alpha(z_{12}) = 1/2\cdot p_l^{x_1} (1 - p_l)^{1-x_1}\$

Calculating \$ \xi \$'s

$$\begin{align}\xi(z_{n-1}, & z_n) = \\ & \frac{\alpha(z_{n-1})p(x_n \given z_n) p(z_n \given z_{n-1}) \beta(z_n)}{p(X)}\end{align}$$

Likelihood calculation

$$p(X) = \sum_{z_n} \alpha(z_n) \beta(z_n) = \sum_{z_N} \alpha(z_N)$$

Example \$ \xi \$ and likelihood

Generic formulas.
Can obtain directly from the transition parameters at each iteration and the values for \$ \alpha \$ and \$ \beta \$.

Computing complexity

\$ K \$ terms in summation, \$ K \$ evaluations for each value of \$z_n\$.
So, each step of \$ \alpha \$ recursion scales like \$ O (K^2) \$.
Since we need to do this for each observation in the chain, the overall complexity is \$ O(K^2N) \$.
Compare to \$ K^N \$ brute force summing out.
Add to this the backwards recursion, likelihood calculation, bookkeeping etc.

Example computing complexity

\$ K = 2 \$, \$ N = 3 \$, so \$ O(12) \$ - longer than brute-forcing it!
But the power quickly dominates when there are more observations.

So, does EM for HMMs converge?

There is no free lunch. Easier computation with EM comes with a price.
Fraction of missing information.
Intuitively, this depends on the number of hidden states.

Properties of EM

Local maximization.
Sensitivity to starting points.
Will explore this in Pset 3.

Announcements

How is pset 3 going?

Resources

Slides nesterko.com/lectures/stat221-2012/lecture11
Class website theory.info/harvardstat221
Class Piazza piazza.com/class#spring2013/stat221
Class Twitter twitter.com/harvardstat221

Final slide

Next lecture: ECM, EM and Bayesian approaches, EM + MCMC